Произведение матриц

Матрицу А, слева, можно умножать на матрицу В, если число столбцов матрицы А равно числу строк матрицы В.

Определение. Произведением матрицы А =(а_ij) размера m ´ k на матрицу в =(в_st) размера k ´ n называется матрица С = АВ =(с_it) размера m ´ n с элементами с_it = a_i1в_1t + a_i2в_2t +···+ a_ikв_kt.

Таким образом, для определения элемента с_it матрицы С = АВ, необходимо i -ю строку матрицы А поэлементно умножить на t -ый столбец матрицы В.

п р и м е р. Найти произведение матриц С = АВ, если:

.

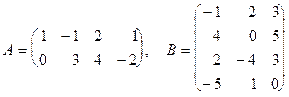решение:

Матрица А имеет размер 2´4, а матрица В - 4´3. Поскольку число столбцов матрицы А равняется числу строк матрицы В, следовательно, матрицу А можно слева умножить на матрицу В. Пусть АВ = С. Тогда:

; ;

;

;

;

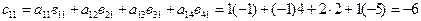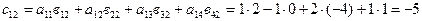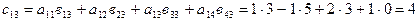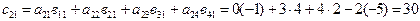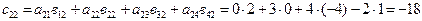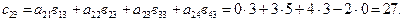
Таким образом, .

Действия с матрицами подчиняются следующим свойствам:

А + В = В + А

К(А + В) = КА + КВ (К - действительное число)

А(В + С) = АВ + АС

А(ВС) = (АВ)С

Примечание. Переместительный (коммутативный) закон для произведения матриц в общем случае не выполняется (если АВ = С, то произведение ВА может вообще не существовать).

Матрицы, для которых выполняется свойство АВ = ВА, называются коммутативными.

Определение. Матрица А^Т = || а_i || называется транспонированной по отношению к матрице А =|| а_i ||. Если матрица А имеет размер m ´ n, то размер матрицы А^Т будет n ´ m.

П р и м е р.

.

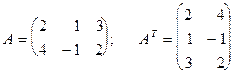Имеют место следующие равенства:

(А^Т)^Т = А;

(А+В)^Т = А^Т +В^Т;

(КА)^Т = КА^Т;

(АВ)^Т = А^ТВ^Т;

DА = DА^Т;

D(АВ) = DА×DВ.

Поиск по сайту: