Обратная матрица. Определение. Матрица А-1 называется обратной матрице А, если имеет место соотношение: А-1А = А А-1 = Е

Определение. Матрица А^-1 называется обратной матрице А, если имеет место соотношение: А^-1А = А А^-1 = Е.

Если матрица имеет обратную матрицу А^-1, то она называется обратимой.

Квадратная матрица А =(а_ij), определитель DА которой отличный от нуля, является обратимой.

Обратная матрица в этом случае выражается соотношением: || А_ji ||, где А_ji - алгебраические дополнения элементов а_ij матрицы А.

Если , то

П р и м е р. Дана матрица . Найти матрицу А^-1, обратную к матрице А. Полученный результат проверить, определяя произведение А^-1А = Е.

Решение:

Найдем определитель матрицы А.

.

Поскольку DА¹0, матрица А является обратимой, т.е. существует обратная матрица А^-1.

Найдем алгебраические дополнения элементов матрицы А:

; ;

; ;

; ;

; ;

.

Таким образом, - матрица, обратная к матрице А. Найдем произведение А^-1А.

.

Поскольку А^-1А = Е, следовательно, обратная матрица А^-1 найдена правильно.

Ответ: .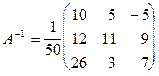

Поиск по сайту: