 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Разложение функций в степенные ряды
Говорят, что функция f (x) разлагается в степенной ряд 
на интервале (- r, r), если на этом интервале данный степенной ряд сходится и его сумма равна f (x), т.е.
f (x) = , х Î (- r, r), r > 0. (12)
Определение 1. Если f (x) на интервале (- r, r) разлагается в степенной ряд, то она называется аналитической функцией. Одна и та же функция f (x) не может иметь двух различных разложений вида (12), т.к. справедлива
Теорема 1. Если функция f (x) разлагается в некотором промежутке в степенной ряд по степеням х, то это разложение единственно.
Коэффициенты ряда (12) определяются по формулам Тейлора:
(13)
2. Определение 2. Степенной ряд с коэффициентами (13), вычисленными по некоторой функции f (x), называется рядом Тейлора этой функции f (x).
Итак, для всякой бесконечно дифференцируемой в (- r, r) функции f (x) можно составить её ряд Тейлора:
,
который часто называют рядом Маклорена.
Необходимо помнить пять основных разложений, а именно:
1. 
.
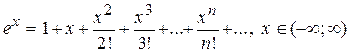2. 
.
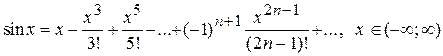3. 
.
4. 
.
5. 
.
Этот ряд называют биномиальным рядом.
Частным случаем при т = - 1 разложения 5 является разложение (сумма геометрической прогрессии):
.
6. 
.
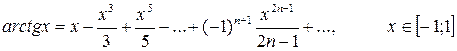Замечание 2. Все рассуждения этого параграфа можно перенести для функции f (х), разлагаемой в ряд по степеням (х - а). Тогда ряд Тейлора примет вид
.
1. Рассмотрим вначале дробно-рациональные функции, которые имеют вид:
где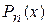 
и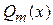 
- многочлены степени n и m, соответственно.
Эти функции можно разложить в степенной ряд, не применяя теоремы 2 и 3, например, следующим путем:
а) разложением функции f (x) на простейшие дроби;
б) преобразованием полученных простейших дробей или в ряд некоторой бесконечно убывающей геометрической прогрессии, или к дроби, являющейся результатом k -кратного дифференцирования ряда этой прогрессии;
в) определением общего промежутка сходимости для всей суммы простейших дробей, т.е. для заданной рациональной функции f (x).
Пример 46. Разложим в ряд Тейлора функцию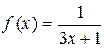 
по степеням (x +1).
Решение. Преобразуем данную функцию так:
.
Используя формулу (5), суммы геометрической прогрессии, получаем при 
, т.е. при 
следующее разложение:
,
или
.
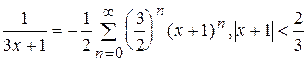Поиск по сайту: