Вопрос. Разложение аналогового сигнала в ряд Фурье

Разложение в ряд Фурье заключается в представление периодического сигнала в виде суммы синусоидальных сигналов.

Пример представления пилообразного сигнала в виде суммы синусоидальных сигналов с различной амплитудой и фазой представлен на рис. 12.

Введем основную частоту периодического сигнала с периодом T: w_1=2pi/T. Периодический сигнал при разложении в ряд Фурье представляется в виде суммы синусоидальных сигналов или гармоник, с частотами кратными основной частоте: 2w_1, 3w_1... Амплитуды этих сигналов называются коэффициентами разложения. Ряд Фурье записывается в виде суммы гармоник:

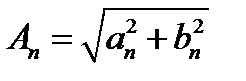
Вещественная форма ряда Фурье:

Используя известную форму записи из курса электротехники в виде комплексного числа, ряд Фурье представляется в виде:

В данное выражение входят гармоники с отрицательными частотами. Отрицательная частота – это не физическое понятие, она связана со способом представления комплексных чисел. Так как сумма гармоник должна быть действительным числом, то каждой гармонике соответствует комплексно сопряженная гармоника с –ω. По абсолютному значению амплитуды гармоники с положительными и отрицательными частотами равны.

Поиск по сайту: