Вопрос. Z – преобразование

Определяется следующим образом:

, где z – комплексная переменная для системы

Z – преобразование – степенной ряд u имеет область сходимости, в которой x(z) – конечная.

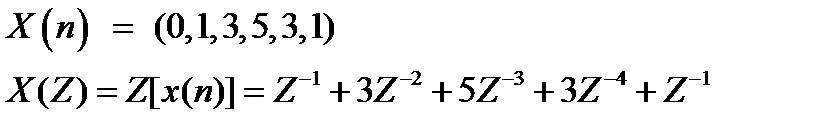
Обратное Z – преобразование позволяет восстановить последовательность по ее z – образу.

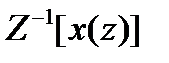
Z – образ можно разложить в степенной ряд:

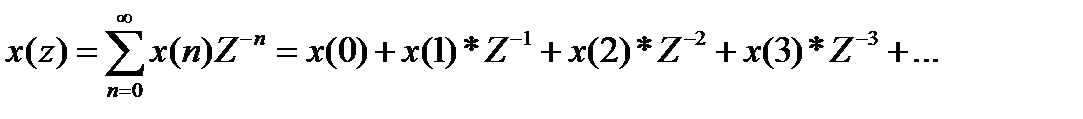
Из данной записи видно, что коэффициенты можно найти как . X(Z) выражается как отношение 2-х многочленов:

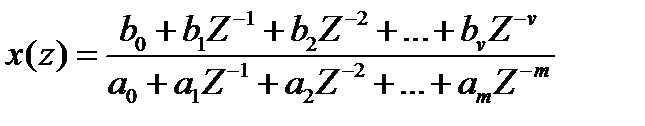
Обратное Z – преобразование может найти отличие 3-х методов: метода разложения в степенной ряд, метод разложения на элементарные дроби, метод вычетов.

Рассмотрим последний метод.

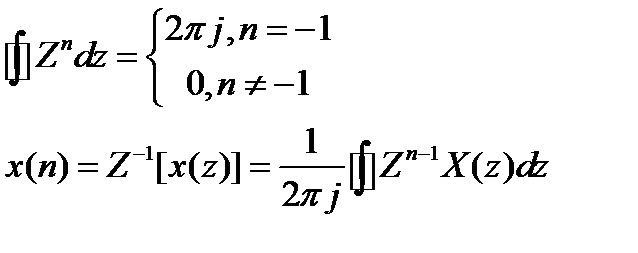
Свойства Z – преобразования:

1. Линейность – Z – преобразование от линейной комбинации 2-х последовательностей равна линейной комбинации Z – преобразования (линейная комбинация – a*x+b*y).

Z – преобразование от сигнала y(t) получена из исходного сигнала x(t) сдвигом на одну позицию в сторону запаздывания, равную Z – преобразованию исходного сигнала, домноженного на .

, где - задержка на длину интервала дискретизации.

2. Дискретная свертка. Сверка двух дискретных сигналов соответствует произведению их Z – преобразований.

Поиск по сайту: