 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Взаимная ортогональность собственных функций эрмитовых операторов
Пусть n≠m и  и
и  – два различных собственных значения вещественной величины
– два различных собственных значения вещественной величины 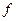 , а
, а 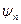 и
и  – соответствующие им собственные функции
– соответствующие им собственные функции
 (II.11)
(II.11)
Умножив первое равенство из (II.11) слева на  , а равенство, комплексно сопряженное второму, на
, а равенство, комплексно сопряженное второму, на 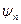 и, вычитая, получившиеся произведения, друг из друга, получим:
и, вычитая, получившиеся произведения, друг из друга, получим:
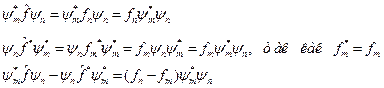
(II.12)
Проинтегрируем последнее равенство по 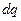 :
:
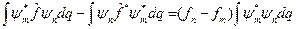 (II.13)
(II.13)
В силу эрмитовости операторов левая часть равенства (II.13) равна нулю и отсюда равна нулю правая часть:
 (II.14)
(II.14)
То есть действительно 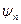 и
и  – взаимно ортогональны.
– взаимно ортогональны.
Сложение и умножение операторов
Поиск по сайту: