Приближение Борна-Оппенгеймера

Суть приближения Борна-Оппенгеймера заключается в разделении движения электронов и ядер. Это легко понять, воспользовавшись простыми рассуждениями с точки зрения классической физики. Очевидно, имея намного меньшую массу по сравнению с массой ядер, электроны в молекуле более подвижны по сравнению с ядрами, то есть их движения совершаются в поле практически неподвижных ядер.[3] За время заметного смещения ядра электрон успевает много раз пройти вокруг него. Именно такая классическая модель позволяет рассматривать движение ядер и электронов в отдельности. Поскольку приближение Борна-Оппенгеймера является квантово -механическим, его нужно обосновать на языке квантовой механики. Для этого вводится параметр малости или малый параметр

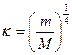(III.1)

m – масса электрона, а M – масса ядра.

По этому параметру малости проводится разложение в ряд гамильтониана и волновой функции. Обозначим совокупность координат ядра через 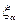, а смещение ядра представим в виде произведения параметра 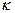и координат ядра :

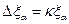
Тогда 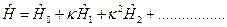(III.2)

Здесь, как обычно при разложении в ряд ,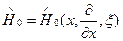

, ,

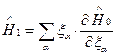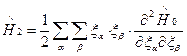где – совокупность координат электронов.

Тогда решение уравнения Шредингера естественно искать в виде:

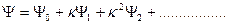(III.3)

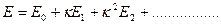(III.4)

Подставим (III.2), (III.3) и (III.4) в стационарное уравнение Шредингера 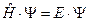и получим совокупность уравнений, соответствующих разным степеням приближений разложения по параметру малости. Нулевое приближение имеет место при решении уравнения

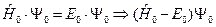(III.5)

Это уравнение для фиксированных ядер и фиксированные координаты ядер 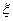входят в него в качестве параметров. Собственные значения уравнения (III.5) 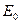являются функциями координат ядер 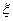. Собственные функции уравнения (III.5) – тоже функции 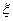с точностью до множителя, не зависящего от координат электронов ,

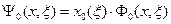(III.6)

Первое приближение получается при решении уравнения вида

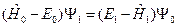(III.7)

В этом легко убедиться, подставив разложение первого порядка для 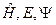в стационарное уравнение Шредингера

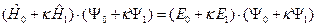(III.8)

Раскрывая скобки, получаем уравнение:

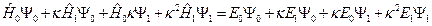Поскольку в левой части уравнения 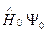= 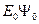, то имеем, сократив члены, содержащие к²

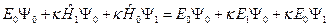(III.9)

Сокращая одинаковые члены 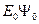, получаем уравнение (III.7). Это линейное неоднородное уравнение. Оно имеет решение только в том случае, когда его правая часть ортогональна к решению левой части, то есть к 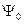(речь идет об ортогональности по переменной ), то есть при условии

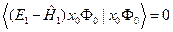, (III.10)

или

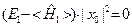, где 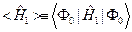(III.11)

Поскольку 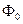не является собственной функцией оператора 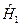, то 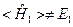. В общем случае 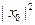≠0 и, значит, равна нулю разность двух не равных друг другу величин. Но это возможно только, если сами эти величины равны нулю, то есть 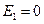и 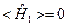. С другой стороны,

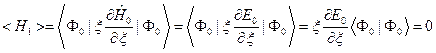(III.12)

Таким образом, в приближении Борна-Оппенгеймера должно выполняться условие:

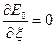(III.13)

Физический смысл этого условия заключается в том, что фиксированные координаты ядер 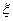, имеют значения, отвечающие экстремальному значению полной энергии системы 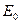, то есть выполняются условия равновесия. Таким образом, правая часть уравнения (III.7) обращается в ноль, то есть

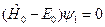(III.14)

Но 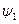не является собственной функцией уравнения (III.14), поэтому оно может удовлетворяться лишь тождественным нулем, то есть 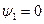. То есть в равновесном состоянии члены первого порядка по 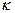отсутствуют. В уравнениях (III.2) - (III.4) члены второго порядка по 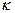достаточно малы, и ими можно пренебречь. Поэтому в приближении Борна-Оппенгеймера можно принять решение вида (III.6). То есть действительно волновая функция может быть записана в виде произведения чисто ядерной и электронной частей, в которые координаты ядер входят в качестве фиксированных параметров. Можно показать, что ошибка, возникающая при использовании приближения Борна-Оппенгеймера невелика.

Приближение, в котором можно провести разделение электронного и ядерного движений и одновременно с этим учитывается слабое взаимодействие между этими двумя типами движений, называется адиабатическим.

Можно сказать, что адиабатическое приближение по сути дела является приближением Борна – Оппенгеймера с учетом слабого взаимодействия между движением ядер и электронов.

Эти два приближения очень близки, но, строго говоря, они разные. В подавляющем большинстве случаев уже само приближение Борна-Оппенгеймера позволяет получить очень хорошее соответствие с экспериментом, то есть описание реальной системы. Адиабатическая поправка к приближению Борна-Оппенгеймера уменьшается с ростом массы ядер. Например, для энергии диссоциации молекулы Н₂ она равна ~0,02%, а для молекулы D₂ ~0,007%. За исключением простых задач (непосредственное значение которых для химии невелико), уравнение Шредингера не может быть решено точно. И в связи с этим мы начали рассматривать основы для использования приближенных методов к его решению. И в качестве такой основы мы рассмотрели приближение Борна-Оппенгеймера, позволяющее разделить движение ядер и электронов.

Отметим, что в более общей формулировке приближение Борна-Оппенгеймера подразумевает возможность разделения также и других видов движений, например, колебательного, поступательного, вращательного, возбуждения ядерного спина и т.д..

До того, как рассматривать методы решения уравнения Шредингера с гамильтонианом, построенным на основе приближении Борна-Оппенгеймера, то есть с неподвижными ядрами, имеет смысл вспомнить о двух основополагающих методах квантовой механики для приближенного решения уравнения Шредингера – вариационном методе и методе теории возмущений. Здесь мы рассмотрим лишь вариационный метод и вариационный принцип, на котором он основан, а метод теории возмущений рассматривается в спецкурсе «Избранные главы квантовой химии».

Поиск по сайту: