Спин электрона

Помимо орбитального углового момента электрону приписывают внутренний угловой момент – так называемый спин. Экспериментально установлено, что его компонента в выделенном направлении может принимать два значения . Согласно Паули, спин электрона можно рассматривать как величину типа углового момента, приписывая ему квантовое число . Именно так постулируется существование спинового момента , не зависящего от орбитального момента .

Существуют операторы и , подчиняющиеся тем же коммутационным соотношениям, что и операторы и .

Например, для компонент оператора спина

(II.39)

И для квадрата оператора спина, который коммутирует с каждой из компонент оператора спина.

(II.40)

Вводя квантовые числа m_s и l_s, определяющие значения проекции спина на любое направление Oz и его квадрат соответственно, мы можем записать формулы квантования спина в полной аналогии с формулами квантования для орбитального момента:

(II.41)

В пренебрежении взаимодействием между спином и орбитальным движением волновую функцию электрона записывают так:

, где обозначает спиновую функцию.

По существу это простой значок, указывающий состояние спина частицы. Смысл этого значка или спиновой функции в том, что индекс α принимает два значения, равных соответственно и . Пишут соответственно α и β или S_α или S_β.

Спиновые функции обладают свойствами ортонормированности:

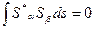(II.42)

(II.43)

В этих уравнениях s – спиновая переменная, которую не следует путать с введённым выше квантовым числом s. Cледует сказать, что невозможно вывести аналитическую форму функций S_α и S_β. На практике спиновая часть одноэлектронной функции учитывается указанием конкретного квантового числа .

Поиск по сайту: