АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Стационарные состояния

Читайте также:
  1. III. Анализ результатов психологического анализа 1 и 2 периодов деятельности привел к следующему пониманию обобщенной структуры состояния психологической готовности.
  2. Агрегатные состояния
  3. Агрегатные состояния и термодинамические фазы
  4. Анализ движения и технического состояния основных средств
  5. Анализ и оценка финансового состояния торговой организации
  6. Анализ состава, динамики и состояния основных средств
  7. Анализ состояния дебиторской задолженности
  8. Анализ состояния запасов
  9. Анализ состояния и эффективности использования основных средств
  10. Анализ состояния и эффективности использования трудовых ресурсов
  11. Анализ состояния производства
  12. Анализ финансового состояния организации

 

В квантовой механике состояния, в которых энергия имеет определенное значение, называются стационарными состояниями. Они описываются волновыми функциями 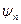, являющимися собственными функциями оператора Гамильтона, то есть

 

, (II.24)

 

где – собственное значение энергии. Это уравнение называется стационарным уравнением Шредингера. Его решению для различных задач посвящена оставшаяся часть разделов квантовой механики и квантовой химии нашего курса. Смысл закона сохранения энергии в квантовой механике заключается в том, что если в данном состоянии энергия имеет определенное значение, то это значение остается постоянным во времени.

Это справедливо для замкнутых систем и систем не находящихся в переменном внешнем поле. В самом деле, поскольку все моменты времени эквивалентны, гамильтониан такой системы не зависит от времени явно.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)