Уравнение Шредингера. Уравнение Шредингера, зависящее от времени (называемое иногда временным уравнением Шредингера), является основным уравнением квантовой механики и выглядит

Уравнение Шредингера, зависящее от времени (называемое иногда временным уравнением Шредингера), является основным уравнением квантовой механики и выглядит следующим образом:

(II.18)

Оно полностью определяет функцию при заданной функции 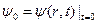в начальный момент времени. В уравнении Шредингера оператор 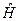– это оператор Гамильтона, получаемый из обычной классической функции Гамильтона путем замены встречающихся в ней координат и импульсов на соответствующие операторы. 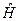называется также гамильтонианом.

Функция Гамильтона в классической механике для одной частицы, находящейся в поле 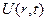, равна сумме кинетической и потенциальной энергий:

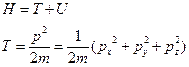
Переход к оператору 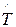должен быть, например, для квадрата компоненты импульса 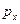, выполнен так:

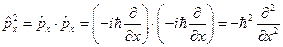
Поэтому оператор кинетической энергии будет равен

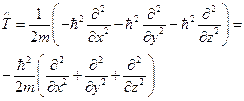
Сумма вторых частных производных называется оператором Лапласа, то есть

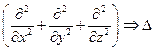и 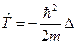(II.19)

Поскольку 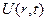есть функция только координат и времени, то действие оператора 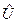этого потенциала является простым умножением соответствующей функции на функцию 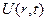. Следовательно, гамильтониан будет в этом случае иметь вид:

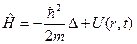(II.20)

Уравнение Шредингера:

(II.21)

Для системы частиц оператор Гамильтона, очевидно, может быть записан так:

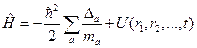. (II.22)

И уравнение Шредингера будет иметь следующий вид:

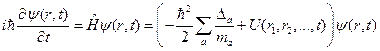(II.23)

Поиск по сайту: