Волновая функция системы

На сегодняшний день наиболее правильным считается статистическое толкование волн де Бройля, предложенное М. Борном. Согласно статистическому толкованию волн де Бройля, их интенсивность в каком-либо месте пространства пропорциональна вероятности обнаружения частицы в этом месте. В этой связи возникает вопрос о способе описания состояния в квантовой механике. Обозначим посредством q совокупность координат всех частиц квантовой системы, а 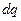– произведение дифференциалов этих координат, которое называют элементом объема конфигурационного пространства системы. Для одной частицы 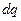совпадает с элементом объема 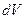обычного пространства. Основу математического аппарата квантовой механики составляет утверждение, что состояние может быть описано определенной (вообще говоря, комплексной) функцией координат . Причем, квадрат модуля этой функции определяет распределение вероятностей значений координат, то есть 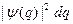– есть вероятность того, что произведенное над системой измерение обнаружит значения координат частицы системы в элементе объема 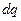конфигурационного пространства системы. Функция называется волновой функцией системы. То есть, если мы знаем волновую функцию системы, то мы знаем о ней все с точки зрения квантовой механики. Иначе говоря, знание волновой функции позволяет в принципе рассчитать вероятности различных результатов измерений, не обязательно измерения координат. Поскольку сумма вероятностей всех возможных значений координат системы должна быть равной 1, имеем:

, где интеграл берется по всему конфигурационному пространству. Это равенство является условием так называемой нормировки волновой функции. Здесь 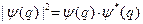, где звёздочка является символом комплексного сопряжения.

Поиск по сайту: