 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
I Функция
Величина, принимающая различные числовые значения, называется переменной.
Если каждому значению переменной величины х, соответствует одно конечное значение величины у, то у называется функцией от х, или зависимой переменной, х называется аргументом, или независимой переменной.
Кратко выражается записью:  или
или  и т.п.
и т.п.
Совокупность значений х, для которых данная функция определена, называется областью существования, или областью определения функции.
Пример. Определить область существования функции  .
.
Решение:Функция определена, если  , Таким образом, область существования функции представляет собой совокупность двух интервалов:
, Таким образом, область существования функции представляет собой совокупность двух интервалов:  и
и  .
.
Если уравнение  может быть однозначно разрешено относительно переменного х, т.е. существует функция
может быть однозначно разрешено относительно переменного х, т.е. существует функция  , такая, что
, такая, что  , то функция
, то функция  , или в стандартных обозначениях
, или в стандартных обозначениях 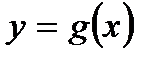 , называется обратной по отношению к
, называется обратной по отношению к  . Очевидно, что
. Очевидно, что  , т.е. функции
, т.е. функции  и
и  являются взаимно обратными.
являются взаимно обратными.
Пример Для функции  определить обратную.
определить обратную.
Решение:  , или
, или  , прологарифмировав, получаем:
, прологарифмировав, получаем:


Функция называется сложной, если ее аргумент в свою очередь есть функция от другой переменной. Пусть  , и
, и  , тогда
, тогда  есть сложная функция или функция от функции. Например,
есть сложная функция или функция от функции. Например,  ,
,  , тогда
, тогда  ;
;  ,
,  , тогда
, тогда  .
.
Функция, заданная уравнением  , не разрешенным относительно зависимой переменной, называется неявной. Например, уравнение
, не разрешенным относительно зависимой переменной, называется неявной. Например, уравнение  определяет у как неявную функцию от х.
определяет у как неявную функцию от х.
Способы задания функции:
Если функция задана одной или несколькими формулами, то говорят, что она задана аналитическим способом.
Функцию можно задать также при помощи графика (графический способ) или при помощи таблицы (табличный способ).
Множество точек (х,у) плоскости ХОУ, координаты которых связаны уравнением  , называется графиком функции.
, называется графиком функции.
Функция у от х называется элементарной, если ее можно задать одной формулой вида  для всех х из области ее определения так, что каждое ее значение может быть получено из постоянных чисел и значения независимой переменной при помощи конечного числа элементарных операций.
для всех х из области ее определения так, что каждое ее значение может быть получено из постоянных чисел и значения независимой переменной при помощи конечного числа элементарных операций.
Основными элементарными функциями называются следующие:
1)степенная функция  , где
, где 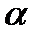 – любое действительное число;
– любое действительное число;
2)показательная функция  ,
,  ;
;
3)логарифмическая функция  ,
,  ;
;
4)тригонометрическая функция  ,
,  ,
,  ,
,  а также
а также  ,
,  ,
,  ,
,  .
.
Свойства функций
Функция называется ограниченной сверху (снизу) в некоторой области значений аргумента, если существует такое число А, что 
 для любого х из этой области. Функция называется ограниченной, если она ограничена и сверху и снизу.
для любого х из этой области. Функция называется ограниченной, если она ограничена и сверху и снизу.
Пример:
1) Функция  определена на всем множестве действительных чисел, ограничена, т.к. при любых значениях х по абсолютной величине не превосходит 1, т.е.
определена на всем множестве действительных чисел, ограничена, т.к. при любых значениях х по абсолютной величине не превосходит 1, т.е.  .
.
| 2) Функция  в промежутке в промежутке  ограничена снизу, например, числом 1, но не ограничена сверху (см. рис.)
3) Функция ограничена снизу, например, числом 1, но не ограничена сверху (см. рис.)
3) Функция  на интервале на интервале  не ограничена, т.е. не ограничена, т.е.  (см. приложение). (см. приложение).
|
Функция  называется возрастающей (убывающей) в некоторой области, если для любой пары чисел
называется возрастающей (убывающей) в некоторой области, если для любой пары чисел  ,
,  , принадлежащей этой области, из
, принадлежащей этой области, из  следует
следует

 .
.
Если же из  следует
следует 
 , то функция
, то функция 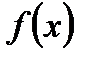 называется неубывающей (невозрастающей).
называется неубывающей (невозрастающей).
Функции, удовлетворяющие первому или второму условиям, называются монотонными.
Пример:функция  возрастает в интервале
возрастает в интервале  ; функция
; функция  убывает на
убывает на  и
и  .
.
Функция  называется четной, если
называется четной, если  , и нечетной, если
, и нечетной, если 
Пример: функция  - четная, т.к.
- четная, т.к. 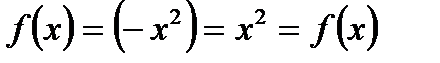 , а функция
, а функция  - нечетная, т.к.
- нечетная, т.к.  . Их сумма
. Их сумма  не является ни четной, ни нечетной (обычно говорят «функция общего вида»)
не является ни четной, ни нечетной (обычно говорят «функция общего вида»)
График четной функции симметричен относительно оси ординат Оу, а график нечетной – относительно начала координат.
Функция  называется периодической, если существует такое положительное действительное число t, что для всех точек х и
называется периодической, если существует такое положительное действительное число t, что для всех точек х и 
 из области определения функции имеет место равенство
из области определения функции имеет место равенство  . При этом число t называют периодом функции. Например, функции
. При этом число t называют периодом функции. Например, функции  и
и  имеют основной период, равный
имеют основной период, равный  , а
, а  и
и  -
-  .
.
Поиск по сайту: