 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Понятие производной функции. Пусть функция y = f(x) определена в некоторой окрестности точки
Пусть функция y = f(x) определена в некоторой окрестности точки 
.
Определение 1: Производной функции f(x) в точке называется предел отношения приращения функции 
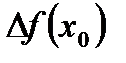к приращению аргумента 
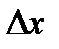при 
, если этот предел существует, и обозначается 
. Итак 
Геометрический смысл производной: Производная функции f(x) в точке равна угловому коэффициенту (тангенсу угла наклона) касательной, проведенной к графику функции в данной точке: 
х
Определение 2: Операция нахождения производной называется дифференцированием.
Определение 3: Функция, имеющая производную в точке , называется дифференцируемой в этой точке. Функция, имеющая производную в каждой точке интервала 
, называется дифференцируемой на этом интервале 
.
Пример: найти производную функции 
в ее произвольной точке
Даем аргументу х приращение 
и найдем приращение функции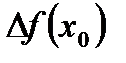
Найдем отношение приращения функции к приращению аргумента:
Найдем предел этого отношения, когда приращение аргумента стремится к нулю, т.е. искомую производную:
Теорема (необходимое условие существования производной). Если функция дифференцируема в точке, то она непрерывна в этой точке.
Утверждение, обратное теореме не верно. Из непрерывности не следует дифференцируемость.
Пример: найти производную функции 
в точке 
Таким образом, в точке х=0 функция непрерывна, но производная не существует.
Поиск по сайту: