Дифференциал независимой переменной

Рассмотрим функцию у=х, dy=dx. Из теорем о связи производной и дифференциала следует, что: dy=1 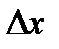, dx= dy= .

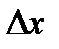Дифференциал независимой переменной равен малому прираще­нию этой переменной.

Таким образом, получена формула для вычисления дифференциа­ла функции: dy = f'(x_o)dx.

Дифференциал функции равен произведению производной функ­ции в данной точке на дифференциал независимой переменной: dy= 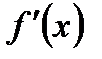dx.

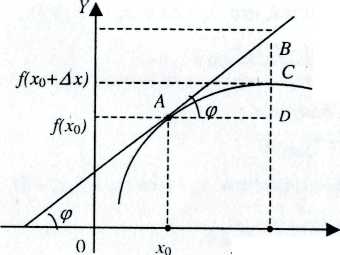
Геометрический смысл дифференциала: Дана дифференцируемая функция y=f(x). Возьмем произвольную точку и проведем в этой точке касательную к графику. Дадим аргу­менту приращение 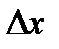. Дифференциал функ­ции в точке равен прираще­нию ординаты касательной, проведенной к графику функ­ции в данной точке , соответствующей приращению ее абсциссы на .

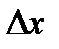х

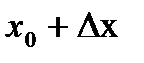
Поиск по сайту: