Свойства непрерывных функций

Функции, непрерывные на отрезке, обладают рядом свойств, которые имеют большое теоретическое и практическое значение. Отметим без доказательства некоторые из них.

Теорема 1 (о промежуточных значениях.) Если непрерывная на отрезке 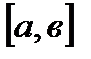функция принимает на концах этого отрезка значения А и В, то на этом отрезке она принимает и все промежуточные значения между А и В.

Следствие. Если функция непрерывна на отрезке 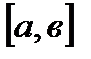и на его концах принимает значения разных знаков, то существует хотя бы одна точка с в интервале, в которой функция обращается в ноль:

Теорема Вейерштрасса (о наибольшем и наименьшем значении функции). Если функция непрерывна на отрезке 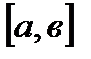, то она достигает на нем своего наибольшего и наименьшего значений.

Контрольные вопросы:

1) Что называется пределом функции?

2) Сформулируйте основные теоремы о пределах.

3) Что называется бесконечно малой и бесконечно большой функцией?

4) Как раскрываются неопределенности , .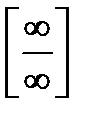

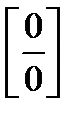5) Запишите 1 и 2 замечательные пределы, в каком случае они используются?

6) Какая функция называется непрерывной в точке?

7) Какая точка называется точкой разрыва I рода, II рода (в чём отличие)?

8) Перечислите основные теоремы о непрерывных функциях.

9) Сформулируйте основные свойства непрерывных функций.

Задания для самостоятельной работы студентов:

Вычислить пределы:

; ; ; ;

; ; ; ;

; ; .

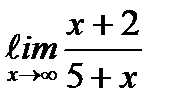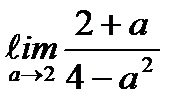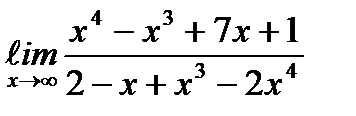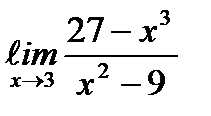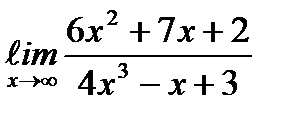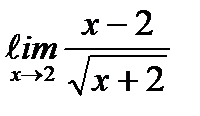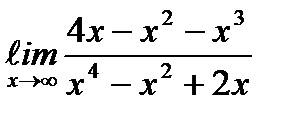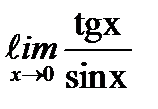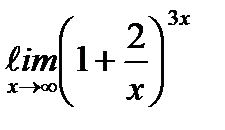Найти точки разрыва и определить их род: , .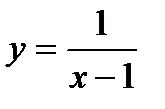

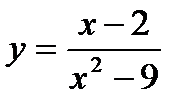Поиск по сайту: