Понятие определенного интеграла

Определение 1: Приращение любой из первообразных функций F(x) + C при изменении аргумента от х=а до х=в функции f (x) называется определенным интегралом и обозначается:

Равенство называется формулой Ньютона-Лейбницы.

Рассмотрим другой подход к введению определенного интеграла. Пусть дана функция f (x), определенная на отрезке [a, b], где . Выполним следующие операции:разобьем отрезок [a, b] на 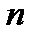частей точками х и обозначим - шагом разбиения, в каждом из отрезков зафиксируем произвольную точку , составим сумму всех произведений.

Если функция f (x) не отрицательна на [a, b], то каждое слагаемое равно площади прямоугольника с основанием и высотой . А вся сумма равна площади «ступенчатой фигуры», получающейся объединением всех прямоугольников.

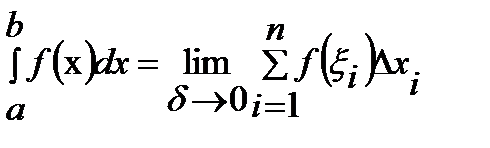Определение 2: Если при любой последовательности разбиений отрезка [a, b], таких что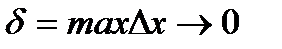 и при любом интегральная сумма стремится к одному и тому же конечному пределу А: , то число А называется определенным интегралом от функции f (x) на отрезке [a, b] и обозначается:

Функция f (x), для которой существует определенный интеграл, называется интегрируемой на отрезке [a, b].

Всякая непрерывная на отрезке [a, b] функция f (x) интегрируема на этом отрезке.

Геометрический смысл: Если интегрируемая на отрезке [a, b] функция неотрицательна, то определенный интеграл численно равен площади криволинейной трапеции, ограниченной графиком функции, осью абсцисс и прямыми х=а и х=в.

Поиск по сайту: