 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Основные теоремы о непрерывных функциях. Теорема 1. Алгебраическая сумма конечного числа непрерывных функций на некотором промежутке есть функция непрерывная на этом промежутке
Теорема 1. Алгебраическая сумма конечного числа непрерывных функций на некотором промежутке есть функция непрерывная на этом промежутке.
Теорема 2. Произведение конечного числа непрерывных функций на некотором промежутке есть функция непрерывная на этом промежутке.
Теорема 3. Частное отделения двух непрерывных функций на промежутке функций, есть функция непрерывная во всех точках этого промежутка. 
Теорема 4. Если функции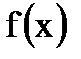 
и 
непрерывны в своих областях определения и область значений функции содержится в области определения функции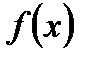 
, то сложная функция 
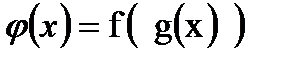непрерывна в своей области определения.
Поиск по сайту: