АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Замечательные пределы

Читайте также:
  1. Виды соучастников. Основания и пределы уголовной ответственности соучастников
  2. Вопрос37. Первый и второй замечательный пределы и следствия из них.
  3. Глава II. Пределы изменчивости характера рас
  4. За пределы слов и звуков
  5. За пределы страны или препятствовать их возвращению на роди-
  6. Законная сила судебного решения (понятие, свойства, пределы).
  7. ЗАМЕЧАТЕЛЬНЫЕ ПРОЦЕССЫ ДВУХ КУПЦОВ
  8. КОНЦЕНТРАЦИОННЫЕ ПРЕДЕЛЫ ВЗРЫВА
  9. Круг органов, уполномоченных осуществлять оперативно-розыскную деятельность; пределы их полномочий
  10. Односторонние пределы функции
  11. Основания ответственности соучастников. Пределы вменения соучастникам объективных и субъективных признаков. Наказание за преступление, совершенное в соучастии.

Для нахождения пределов тригонометрических функций (, , , ) используется первый замечательный предел и следствие из этого предела.

 

Первый замечательный предел: Предел отношения синуса малой дуги к самой дуге, выраженной в радианах, при стремлении величины дуги к нулю равен единице:

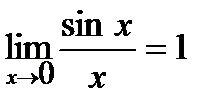
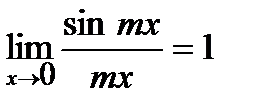
Следствие 1-го замечательного предела: .

Пример: .

 

Для нахождения числа е и раскрытия неопределенности 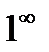используется 2-ой замечательный предел.

Второй замечательный предел: Предел последовательности при равен 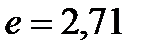: или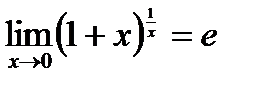

Пример: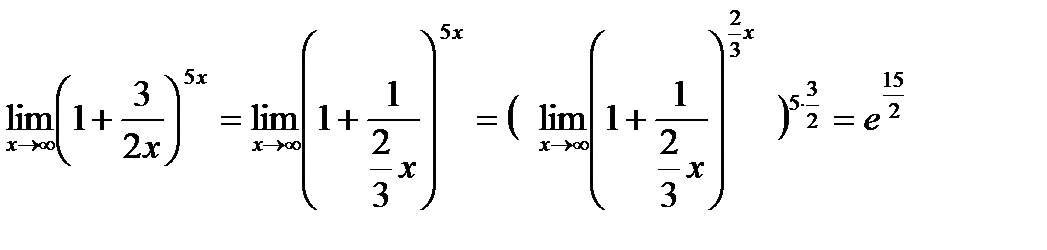


В решении задач теории пределов могут быть полезны следующие равенства: .

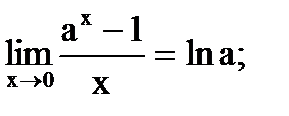
Можно также заменять бесконечно малые величины эквивалентными им:


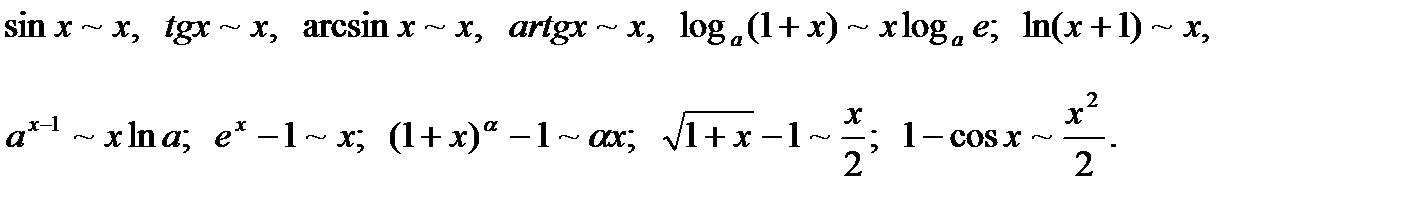
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)