 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Методы интегрирования
Неопределенные интегралы рассчитываются тремя методами.
1. Интегрирование в случаях, когда удается сразу воспользоваться табличными интегралами, называют непосредственным. Метод непосредственного интегрирования заключается в преобразовании подынтегральной функции и применении свойств неопределенного интеграла для приведения к табличным интегралам.
Пример: 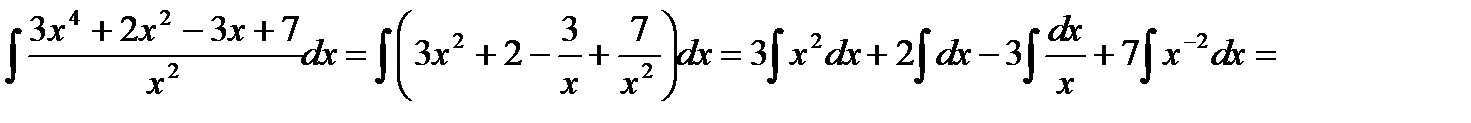
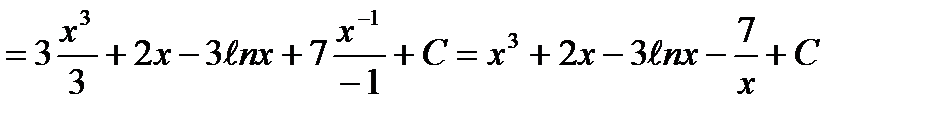
2. Метод подстановки заключается в том, что путем введения новой переменной удается свести заданный интеграл к новому интегралу, который берется непосредственным интегрированием.
Сделаем замену переменной интегрирования х, положив x = j(t) (j(t) – непрерывная функция с непрерывной производной, имеющая обратную функцию).
Тогда  и
и  =
= 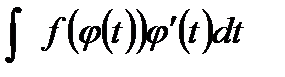
Подразумевается, что после интегрирования в правой части равенства вместо t будет подставлено его выражение через х (возвращение к исходной переменной). Функцию j(t) следует выбирать так, чтобы вычисление интеграла в правой части было максимально простым.
Пример: 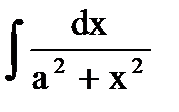 . Положим х = аt, откуда dx = а dt, t=x/a. Исходный интеграл примет вид
. Положим х = аt, откуда dx = а dt, t=x/a. Исходный интеграл примет вид  =
=  =
= 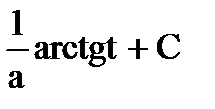 =
=  Т.о
Т.о 
Рассмотрим другой пример:
 [cosx = t; sinxdx = –dt ] =
[cosx = t; sinxdx = –dt ] = 
3. Метод интегрирования по частям заключается в том, что подынтегральное выражение  представляется в виде произведения множителей
представляется в виде произведения множителей  и
и  , при этом
, при этом  входит в
входит в  . В результате заданный интеграл находят по частям: сначала находят
. В результате заданный интеграл находят по частям: сначала находят  , а затем
, а затем  . Таким образом, используется формула:
. Таким образом, используется формула: 
При вычислении интегралов методом интегрирования по частям главным является разбиение подынтегрального выражения на  и
и  . Существуют несколько типов интегралов:
. Существуют несколько типов интегралов:
1. Подынтегральное выражение содержит многочлен относительно переменной х и функции, для которых существует табличная первообразная (например cos аx; sin аx и др.), тогда за  выбирают многочлен, а за
выбирают многочлен, а за  все остальные множители.
все остальные множители.
2. Подынтегральное выражение содержит многочлен относительно переменной х и функцию, для которой не существует табличных интегралов, тогда за  выбирают многочлен, умноженный на
выбирают многочлен, умноженный на  , а за
, а за  принимают функцию, для которой нет табличной первообразной, но можно найти дифференциал
принимают функцию, для которой нет табличной первообразной, но можно найти дифференциал  .
.
3. В некоторых видах интегралов за функцию  можно принимать любой из множителей подынтегрального выражения, если каждый из них имеет табличную первообразную.
можно принимать любой из множителей подынтегрального выражения, если каждый из них имеет табличную первообразную.
Пример:
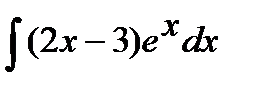 [ и=2х-3; dи =2 dx;
[ и=2х-3; dи =2 dx;  ] =
] = 
 . Таким образом
. Таким образом 
 [ и=
[ и=  ; dи=1/х dx;
; dи=1/х dx;  ] Тогда
] Тогда 

Контрольные вопросы:
1) Сформулируйте определение первообразной функции.
2) Что называется неопределённым интегралом? Каков его геометрический смысл?
3) Сформулируйте свойства неопределенных интегралов.
4) Каковы основные методы интегрирования функций?
5) В чем заключается метод подстановки?
6) Укажите целесообразные подстановки для отыскания интегралов: 
7) Выведите формулу интегрирования по частям.
8) Укажите некоторые типы интегралов, которые удобно вычислять методом интегрирования по частям.
Задания для самостоятельной работы студентов:
1) Найти неопределённые интегралы 1)  ; 2)
; 2)  и указать верный ответ:
и указать верный ответ:
1) а)  б)
б)  2) а)
2) а)  ; б)
; б)  .
.
2) Найти неопределённые интегралы 1)  , 2)
, 2)  и указать верные ответы:
и указать верные ответы:
1) а)  ; б)
; б) 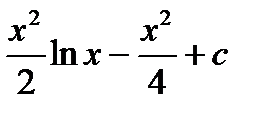 ;
;
2) а)  ; б)
; б) 
3) Вычислить интегралы:
 ;
;  ;
;  ;
; 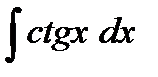
 ;
; 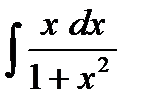 ;
;  ;
; 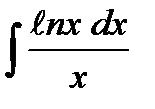 ;
; 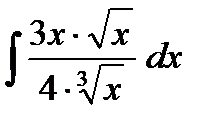 ;
;  ;
; 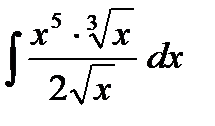 ;
;  ;
; 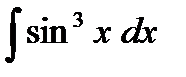 ;
;  ;
; 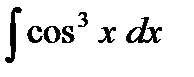 ;
;  ;
; 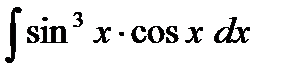 ;
;  ;
; 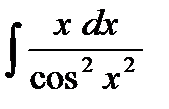 ;
;  ;
;  ;
;  .
.
Поиск по сайту: