АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Правила дифференцирования. Нахождение производной функции непосредственно по определению занимает много времени

Читайте также:
  1. B3.4. Правила оформления графиков
  2. I. Правила терминов
  3. Будова, призначення та правила використання порошкових вогнегасників.
  4. Виды нотариальных действий и правила их совершения
  5. Виола лишь снова переглянулась с Нейтаном и отвернулась в сторону женщины, которая рассказывала о правилах на балу.
  6. Возрастной признак субъекта преступления. Правила установления возраста субъекта. Возрастная невменяемость
  7. Вопрос 4. Правила ведения визуальной ориентировки.
  8. Вопрос №7. общие правила назначения админ-х наказаний
  9. Вставьте определенный, неопределенный или нулевой артикль. Выполните это упражнение письменно. В случае сомнений обратитесь к правилам.
  10. ГЛАВА 1. ПРАВИЛА
  11. Глава 2. Три золотых правила психогигиены
  12. Глава 4.5. Правила работы в СИЗОД.

Нахождение производной функции непосредственно по определению занимает много времени. Поэтому на практике применяют правила дифференцирования.

- Производная постоянной функции равна нулю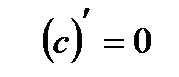

- Если функции и, v, w дифференцируемы в некоторой точке, то и их алгебраическая сумма также дифференцируема в этой точ­ке, причем производная алгебраической суммы равна алгебраической сумме производных и выполняется равенство:

(и + v — w)'= u'+v'-w'.

- Если функции и и v дифференцируемы в некоторой точке, то и их произведение также дифференцируемо в этой точке, при­чем выполняется равенство:

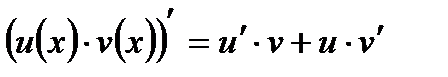
- Постоянный множитель можно выносить за знак про­изводной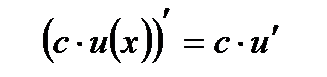

- Если функции и и v дифференцируемы в некоторой точке и функция v в этой точке отлична от нуля, то существует произ­водная частного в этой точке, причем

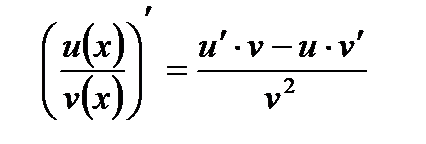
Пример: найти производные функций: , ,


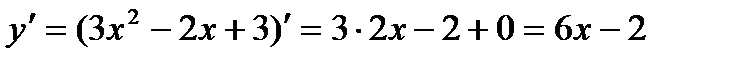
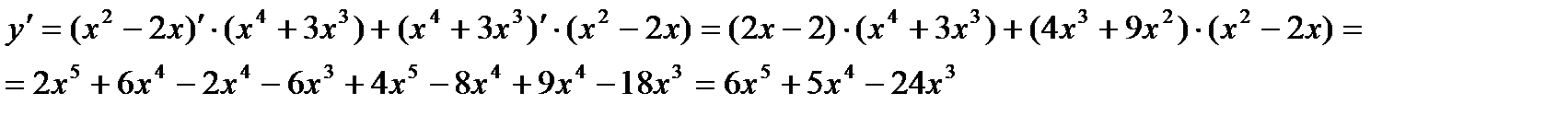
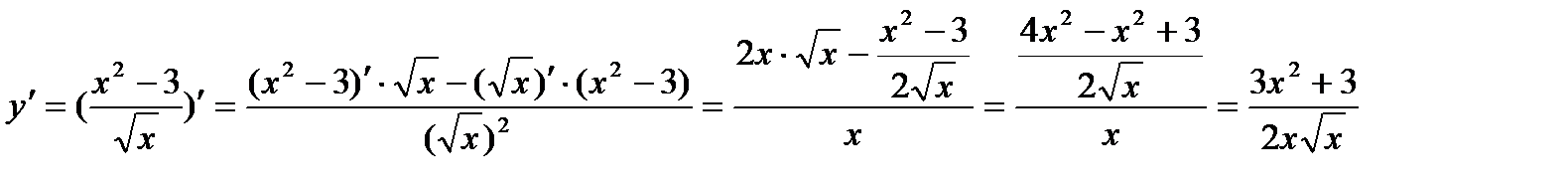
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)