 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Теоремы о пределах
Теорема о существовании предела: Функция не может иметь двух различных пределов в одной точке.
Теорема 1. Предел постоянной равен самой постоянной: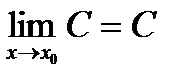 
Теорема 2. Если каждое слагаемое алгебраической суммы функций имеет предел при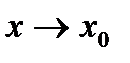 
, то и алгебраическая сумма имеет предел при 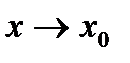, причем предел алгебраической суммы равен алгебраической сумме пределов: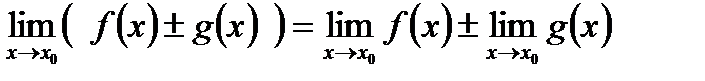 
Теорема 3. Если каждый из сомножителей произведения конечного числа функций имеет предел при 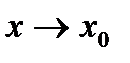,то и произведение имеет предел при 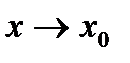, причем предел произведения равен произведению пределов: 
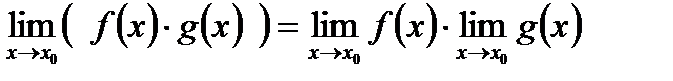
Следствие 1. Постоянный множитель можно выносить за знак предела:
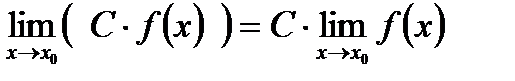
Следствие 2. Предел степени равен степени предела: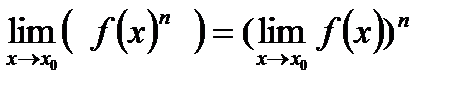 
Теорема 4. Если функции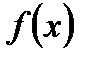 
и 
имеют пределы при 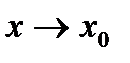,причем 
, то и их частное имеет предел при 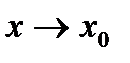,причем предел частного равен частному пределов:
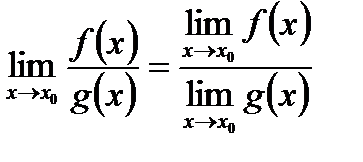
Поиск по сайту: