 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Выпуклость графика функции. Точки перегиба графика
Определение 1. График функции y=f(x) называется выпуклым (вогнутым) на интервале (а, в), если касательная к графику, проведенная в любой точке этого интервала, расположена над (под) графиком функции.
Выпуклый график (
) Вогнутый график (
)
Теорема 1 (достаточное условие выпуклости графика функции). Если вторая производная дважды дифференцируемой функции на некотором интервале отрицательна (положительна), то график функции на данном интервале выпуклый (вогнутый).
Верна и обратная теорема.
Исследовать на выпуклость график функции y=f(x) означает найти те интервалы из области ее определения, в которых вторая производная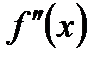 
сохраняет знак.
Заметим, что 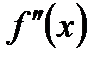может менять свой знак лишь в тех точках, где она обращается в нуль, или в тех точках, где она не существует. Эти точки называются критическими точками второго рода.
Определение 2. Точки, в которой график функции меняет направление выпуклости, называют точками перегиба графика функции.
Точка а является точкой перегиба, а точка с нет, так как в этой точке функция не дифференцируема.
Теорема 2. (необходимое условие существования точки перегиба). Если точка 
является точкой перегиба графика дважды дифференцируемой функции,то в этой точке вторая производная равна нулю: 
Определение 3. Точки, в которых вторая производная равна нулю илине существует, называются критическими точками второй производной. Если функция имеет точки перегиба, то они могут быть тольков критических точках.
Теорема 3 (достаточное условие существования точки перегиба). Если вторая производная дважды дифференцируемой функции в некоторой точке равна нулю и при переходе через нее вторая производная меняет знак, то данная точка является точкой перегиба.
Пример: Исследовать на выпуклость график функции и найти точки перегиба: 
Данная функция определена на всей числовой прямой. Найдем критические точки второго рода:
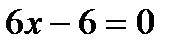
х =1 критическая точка второго рода. Методом пробных точек определяем знак второй производной в каждом из интервалов 
, 
.
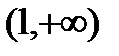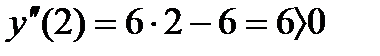
Следовательно, на интервале график обращен выпуклостью вверх, на интервале 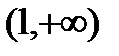вогнут. Точка х=1 является точкой перегиба, т.к. 
сменила знак с «-«на «+».
Поиск по сайту: