 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Методы интегрирования. 1) Метод подстановки. Пусть функцияf (x) непрерывная на отрезке [a, b], функция x = j(t) имеет непрерывную производную на
1) 
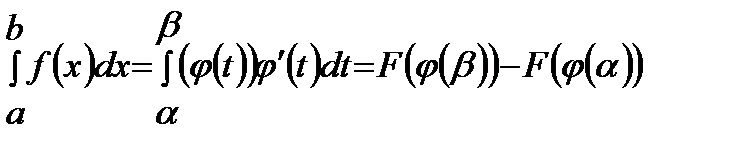Метод подстановки. Пусть функция f (x) непрерывная на отрезке [a, b], функция x = j(t) имеет непрерывную производную на 
, множеством значений функции x = j(t) является отрезок [a, b], 
и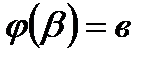 
. Тогда
При вычислении определенного интеграла способом подстановки новая переменная вводится подобно вычислению неопределенного интеграла. Однако в полученном результате не нужно возвращаться к прежней переменной в отличие от неопределенного интеграла.
Пример:
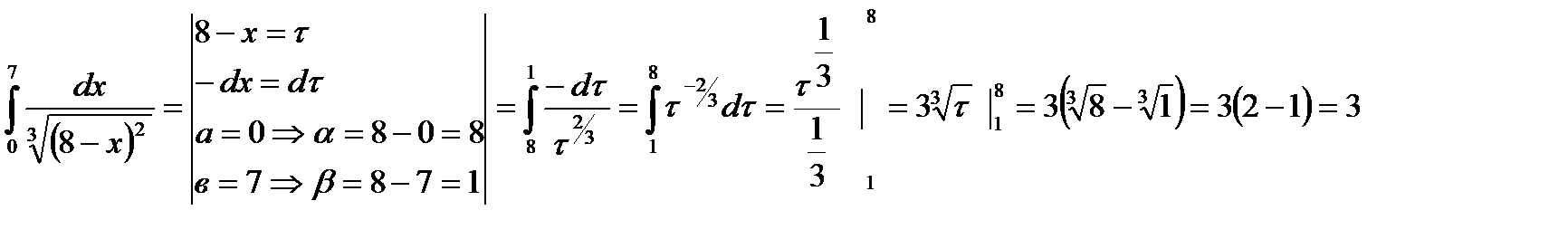
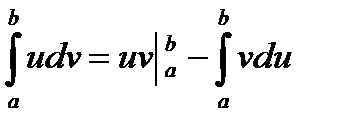2) Метод интегрирования по частям. Пусть функции и и v имеют непрерывные производные на отрезке [a, b]. Тогда интегрируя обе части равенства 
в пределах от а до в получим
Это формула называется формулой интегрированием по частям для определенного интеграла.
Пример:
Поиск по сайту: