Общая схема исследования функции. 1. Определить область определения функции

1. Определить область определения функции.

2. Проверить является функция четной или нечетной.

Функция называется четной, если для любого из области определения функции.

Функция называется нечетной, если

3. Исследовать функцию на периодичность.

Функция 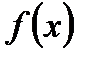называется периодичной, если существует такое число , что для любого из области определения функции выполняется равенство .

4. Исследовать функцию на непрерывность, найти точки разрыва.

Функция непрерывна, если приращение функции стремится к нулю, при , то есть если , то функция непрерывна.

Точки, в которых не существует или равен , называются точками разрыва.

5. Найти критические точки 1 рода.

Для этого определить производную функции и приравнять ее к нулю

(). Критическими называются точки, в которых или не существует.

6. Найти интервалы монотонности и экстремумы функции.

Для этого методом пробных точек в каждом интервале определяют знак .

Если , то функция на этом интервале возрастает, если , то убывает.

Точка, при переходе через которую меняется знак производной , называется экстремумом.

Если меняет знак с «+» на «-» это максимум, если с «-» на «+» точка называется минимумом.

7. Найти критические точки 2 рода.

Для этого определить вторую производную 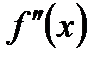и приравнять ее к нулю

().

Критическими точками называются точки, в которых или не существует.

8. Найти интервалы выпуклости и точки перегиба.

Для этого методом пробных точек определяют знак в каждом интервале, образованном критическими точками 2 рода.

Если , то график обращен выпуклостью вверх. Если , то график обращен выпуклостью вниз.

Точка, где меняет знак, называется точкой перегиба.

9. Найти асимптоты графика функции.

Прямая называется наклонной асимптотой. Ее коэффициенты рассчитываются по формулам: , .

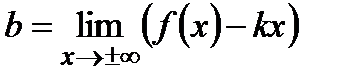Прямая называется вертикальной асимптотой, если предел слева или предел справа .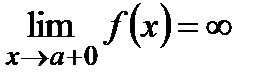

10. Найти точки пересечения графика с осями координат.

11. Построить график функции.

Контрольные вопросы:

1) Как найти интервалы возрастания и убывания функции?

2) Чем характеризуется возрастание и убывание функции y=f(x) в некотором интервале?

3) Какие точки называются критическими?

4) Что называют точками экстремума функции и как находятся?

5) Как найти наибольшее и наименьшее значение функции?

6) Как найти интервалы выпуклости, вогнутости графика функции, точки перегиба?

7) Что называют асимтотой кривой y=f(x)?

8) Перечислите основные этапы исследования функции по общей схеме.

Задания для самостоятельной работы студентов:

1) Найти наибольшее и наименьшее значения функции на отрезке .

2) Исследовать на выпуклость график функции и найти точки перегиба: ,

3) Найти уравнение вертикальной асимптоты кривой: , .

4) Исследовать функцию: , .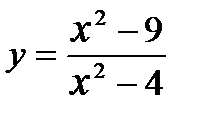

Поиск по сайту: