 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Решение систем линейных уравнений методом Крамера
Рассмотрим систему двух линейных уравнений с двумя неизвестными
 (1.9)
(1.9)
Составим из коэффициентов при неизвестных и свободных членов три определителя 
 и
и 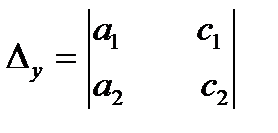 (1.10)
(1.10)
Легко видеть, что второй и третий определители получаются из первого заменой столбца соответствующих индексу коэффициентов столбцом свободных членов. Правило Крамера решения системы линейных уравнений заключается в использовании соотношений  ;
;  (1.11) Отметим, что использовать их можно при ∆ ≠ 0. Это тот случай, когда система определена и совместна (т.е. имеет единственное решение).
(1.11) Отметим, что использовать их можно при ∆ ≠ 0. Это тот случай, когда система определена и совместна (т.е. имеет единственное решение).
Если ∆ = 0, а хотя бы один из определителей ∆x, ∆y отличен от нуля ((∆x)2+(∆y)2 ≠ 0), то система несовместна (т.е. не имеет решений), а если D = ∆x = ∆у = 0, то система неопределена и имеет бесконечное множество решений.
Аналогично правило Крамера формулируется и для системы из трех (или n) линейных уравнений с тремя (или n) неизвестными.
 (1.12) Þ
(1.12) Þ  (1.13')
(1.13')  (1.14')
(1.14')
А Dx, Dy, Dz получаются из D заменой столбца соответствующих коэффициентов столбцом свободных членов. Аналогично проводится и исследование системы (возможны те же три случая).
Контрольные вопросы:
1) Что представляют собой системы 2-х, 3-х, n линейных уравнений переменных с n неизвестными?
2) Каково условие определённости и неопределённости совместной системы?
3) Какой вид имеют формулы Крамера и в каком случае они применяются?
4) При каком условии система линейных уравнений имеет единственное решение?
Задание для самостоятельной работы студентов:
Решить с помощью определителей системы уравнений и указать верные ответы:
1)  2)
2) 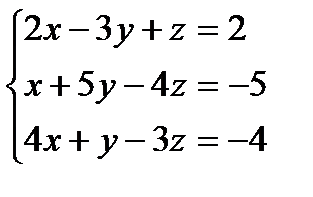
1) а)  ; б)
; б)  ; 2)а)
; 2)а)  ; б)
; б)  .
.
Поиск по сайту: