Производные обратной и неявной функций

Теорема 2: Если функция обратима на интервале (а, в) и имеет отличную от нуля производную в точке х, то ее обратная функция дифференцируема в некоторой точке у: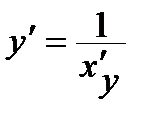

Пример: найти производную функции: а) б)

а) Функция имеет обратную функцию: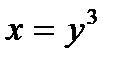

Найдем производную функции: 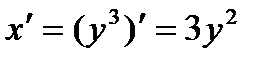. Отсюда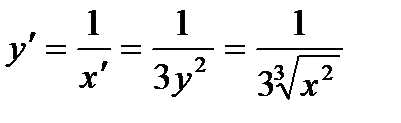

б) Функция имеет обратную функцию:

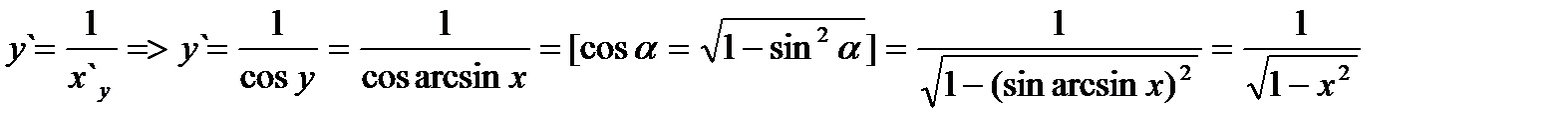
Чтобы найти производную неявной функции у по аргументу х, заданной уравнение, дифференцируем по х левую часть уравнения , считая у функцией от х, и результат приравниваем к нулю. Получаем линейное уравнение, из которого находим искомую производную .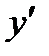

Пример: найти производные функций: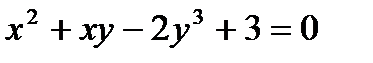

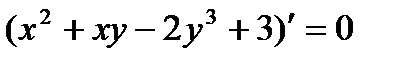
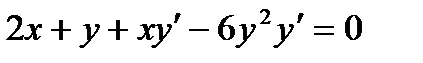
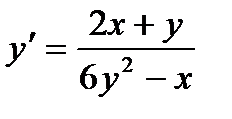
Поиск по сайту: