Асимптоты графика функции. Графики некоторых функции расположены на плоскости так, что они неограниченно приближаются к некоторой прямой

Графики некоторых функции расположены на плоскости так, что они неограниченно приближаются к некоторой прямой. Эти прямые на­зываются асимптотами к графику функции.

Определение 1. Прямая х=а называется вертикальной асимптотой к графику функции y=f(x), если хотя бы один из односторонних равен :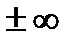

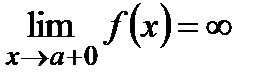
Как правило, в точке а функция терпит разрыв второго рода.

Определение 2. Прямая у=в называется, горизонтальной асимпто­той к графику функции y=f(x), если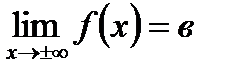

Определение 3. Прямая y=kx+b называется наклонной асимптотой к графику функции у=/(х), если функцию можно представить в виде f(x)=kx+b+ а(х), где а(х) - б.м. при .

Найдем параметры наклонной асимптоты по формулам:

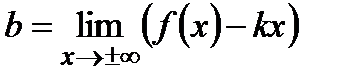
Пример: Найти асимптоты кривой: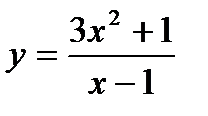

точка разрыва 2 рода, т.к.

,

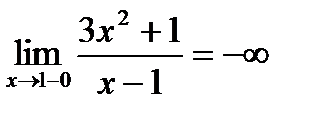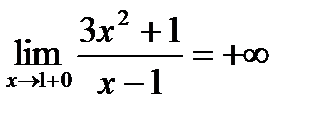
следовательно, х=1 вертикальная асимптота.

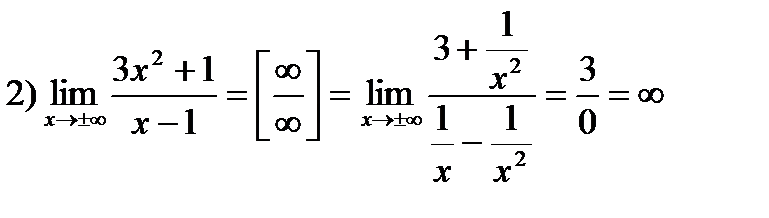
следовательно, горизонтальной асимптоты нет.

3) Найдем коэффициенты наклонной асимптоты:

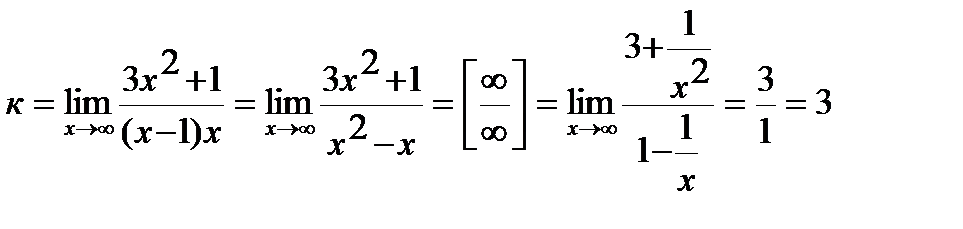
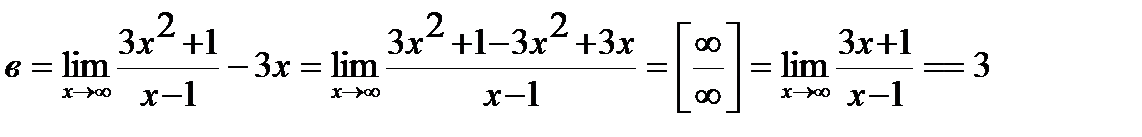
Наклонная асимптота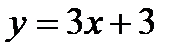

Поиск по сайту: