Производные высших порядков. Дана функция y=f(x), дифференцируемая на интервале (а, в), т.е

Дана функция y=f(x), дифференцируемая на интервале (а, в), т.е. на этом интервале она имеет производную , являющуюся некото­рой функцией от х, которая называется производной первого порядка или первой производной. Предположим, что эта функция также дифференци­руема на интервале (а, в). Тогда ее производная называется второй про­изводной от исходной функции или производной второго порядка. Полученная функция мо­жет вновь оказаться дифференцируемой. Тогда ее производная называ­ется третьей производной или производной третьего порядка: .

Определение: Производной п -го порядка функции y=f(x), если она существует, называется производная от производной (n-1)- гoпорядка: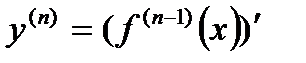

Пример: найти производные функций: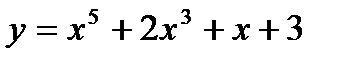

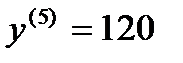
Поиск по сайту: