 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Формула трапеций
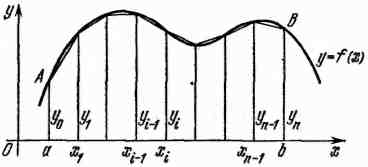
При вычислении интеграла с помощью формулы трапеций подынтегральная функция заменяется функцией, график которой представляет собой ломаную линию, звенья которой соединяют концы ординат. В этом случае площадь криволинейной трапеции аАВв считают приближенно равно сумме площадей обычных трапеций:
Пример: Вычислить интеграл 
по формуле трапеций при 
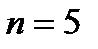. Определимшаг 
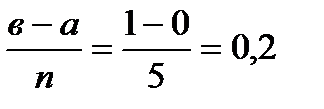. Зададим таблицей значения функции 
:
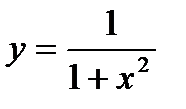| шаг | Х | Х2 | У |
| 1 | |||
| 0,2 | 0,04 | 0,9615 | |
| 0,4 | 0,16 | 0,8621 | |
| 0,6 | 0,36 | 0,7353 | |
| 0,8 | 0,64 | 0,6098 | |
| 0,5 |
По формуле трапеций вычислим интеграл:
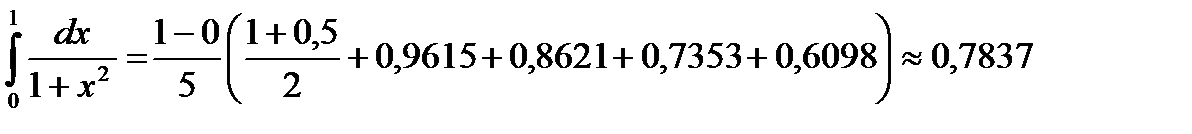
Произведем проверку, рассчитаем интеграл по формуле Ньютона-Лейбница:
5. Вычисление площадей плоских фигур с применением определенного интеграла
Для вычисления площади плоской фигуры достаточно вычислить определенный интеграл, т.к. геометрически определенный интеграл 
численно равен площади S криволинейной трапеции, ограниченной графиком функции 
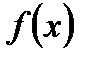, осью абсцисс 
и прямыми 
, 
.
1. Если фигура ограничена графиком непрерывной и неотрицательной функции
(
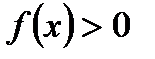) на отрезке 
, то 
. Если 
на отрезке , то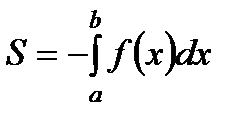 
.
2. Если фигура ограничена графиками двух непрерывных на отрезке функций и 
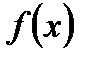,и прямыми , , где 
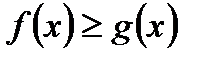и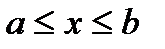 
, то искомая площадь 
. В этом случае предварительно находят пределы интегрирования 
и 
, для этого 
и находят 
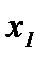и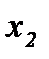 
(
).
3. Если фигура ограничена графиками трех и более непрерывных на отрезке функций, то в этом случае искомая площадь представляется в виде алгебраической суммы площадей, вычисление каждой из которых сводится к одному из предыдущих случаев: 
, где 
.
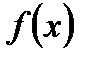Для этого достаточно вычислить определенный интеграл, т.к. определенный интеграл численно равен площади S криволинейной трапеции, ограниченной графиком функции , осью абсцисс и прямыми , .
4. Если фигура ограничена графиком непрерывной и неотрицательной функции (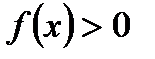) на отрезке , то . Если на отрезке , то .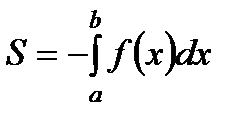
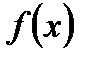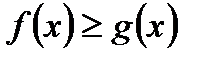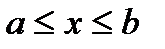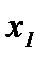5. Если фигура ограничена графиками двух непрерывных на отрезке функций и ,и прямыми , , где и , то искомая площадь . В этом случае предварительно находят пределы интегрирования и , для этого и находят и ().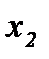
6. Если фигура ограничена графиками трех и более непрерывных на отрезке функций, то в этом случае искомая площадь представляется в виде алгебраической суммы площадей, вычисление каждой из которых сводится к одному из предыдущих случаев: , где .
Пример: Вычислить площадь фигуры, ограниченной линией, заданной функцией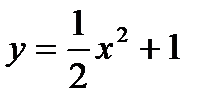 
и прямыми 
, 
, 
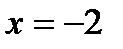Достаточно вычислить определенныйинтеграл 
у.е.
Контрольные вопросы:
1) Что представляет собой определенный интеграл?
2) Запишите формулу Ньютона-Лебница.
3) Сформулируйте свойства определенного интеграла.
4) Перечислите методы нахождения определенного интеграла.
5) Что представляет собой метод подстановки?
6) В чем заключается интегрирование по частям?
7) Какие формулы используются при приближенном вычислении определенных интегралов.
8) Назовите области применения определенного интеграла.
Задания для самостоятельной работы студентов:
Вычислите определенные интегралы:
; 
; 
; 
; 
.
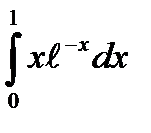Поиск по сайту: