Действия с матрицами. Матрицы одинакового размера можно складывать, получая новую матрицу того же размера по формуле:

1.1 Сложение матриц

Матрицы одинакового размера можно складывать, получая новую матрицу того же размера по формуле:

(1.1)

1.2 Умножение матрицы на число

Произведением числа a на матрицу А называют матрицу определяемую равенством: 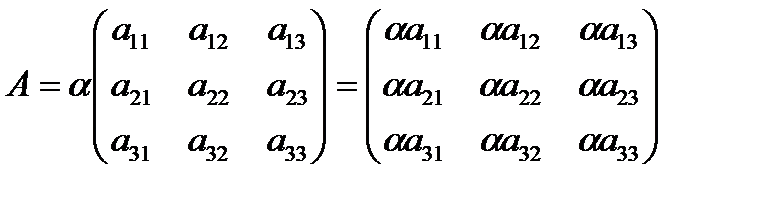(1.2)

2.3 Умножение матриц

Умножение матриц возможно в том случае, если число столбцов умножаемой матрицы равно числу строк матрицы множителя. Размер матрицы-произведения определяется соотношением (m n) (n k)=(m k). Произведение матриц А и В, обозначаемое АВ находят по правилу:

(1.3)

т.е. элемент матрицы – произведения, стоящий в i – й строке и к – ом столбце, равен сумме произведений соответственных элементов i – й строки матрицы А и к – ого столбца матрицы В.

Пример: Найти произведение матриц

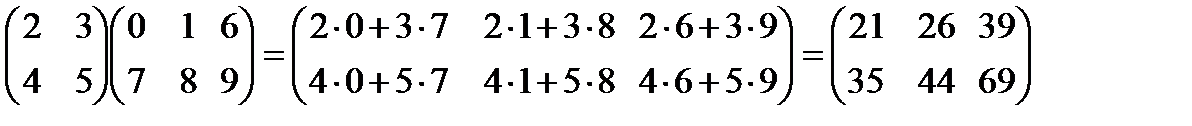
Отметим, что переместительный закон для произведения матриц в общем случае не выполняется: АВ ¹ ВА.

Поиск по сайту: