 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Определение непрерывности функции
Пусть функция y = f(x) определена в некоторой окрестности точки 
Определение 1: Функция y = f(x) называется непрерывной в точке  если для любого
если для любого 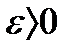 найдется
найдется 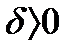 такое, что при всех х, удовлетворяющих неравенству
такое, что при всех х, удовлетворяющих неравенству  , будет выполняться неравенство
, будет выполняться неравенство  .
.
Или Функция y = f(x) называется непрерывной в точке  если она определена в некоторой окрестности точки
если она определена в некоторой окрестности точки  , существует предел функции при
, существует предел функции при 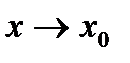 и он равен значению функции в этой точке:
и он равен значению функции в этой точке: 
Определение 2: Функция y=f(x) называется непрерывной на некотором промежутке, если она непрерывна в каждой точке этого промежутка.
Исходя из определений и свойств предела и непрерывности функции, можно доказать непрерывность основных элементарных функций.
Определение 3: Точки, в которых нарушается непрерывность функции, называются точками разрыва.
Определение 4: Точка разрыва  называется точкой разрыва первого рода, если существуют конечные односторонние пределы в этой точке.
называется точкой разрыва первого рода, если существуют конечные односторонние пределы в этой точке.
Определение 5: Точка разрыва  называется точкой разрыва второго рода, если она не является точкой разрыва первого рода, т.е. хотя бы один из односторонних пределов не существует или равен
называется точкой разрыва второго рода, если она не является точкой разрыва первого рода, т.е. хотя бы один из односторонних пределов не существует или равен  .
.
Пример: Исследовать на непрерывность функцию  в точке х =0
в точке х =0
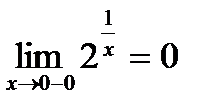 , т.к.
, т.к.  , то
, то 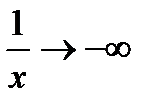 , а
, а 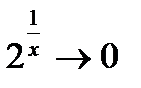
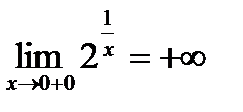 , т.к.
, т.к.  , то
, то  , а
, а 
Таким образом, х =0 точка разрыва второго рода.
Рассмотрим функцию y = f(x) на интервале 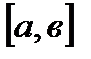 . Возьмем произвольную точку
. Возьмем произвольную точку  из данного интервала. Для любого х из интервала
из данного интервала. Для любого х из интервала 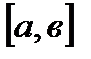 разность
разность  называется приращением аргумента х в точке
называется приращением аргумента х в точке  . Таким образом
. Таким образом 
Разность  называется приращением функции f(x) в точке
называется приращением функции f(x) в точке  .
.
Определение 6: Функция y = f(x) непрерывна в точке  тогда и только тогда, когда приращение функции в точке
тогда и только тогда, когда приращение функции в точке  стремится к нулю, если приращение аргумента стремится к нулю
стремится к нулю, если приращение аргумента стремится к нулю

Пример: Исследовать на непрерывность функцию 
Зададим аргументу х приращаение, тогда приращение функции:

Найдем предел приращения функции при  :
:
 при всех х, кроме нуля.
при всех х, кроме нуля.
Таким образом, функция непрерывна во всех точках области определения, точка х=0 является точкой разрыва.
Найдем пределы функции  слева и справа в точке х =0:
слева и справа в точке х =0: 

Таким образом, точка х =0 является точкой разрыва второго рода.
Поиск по сайту: