 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Предел частного в точке
При вычислении предела частного 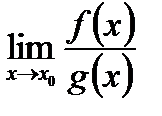 , необходимо проверить обращается ли в ноль предел делителя (
, необходимо проверить обращается ли в ноль предел делителя (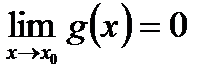 ). Затем рассчитать предел числителя:
). Затем рассчитать предел числителя: 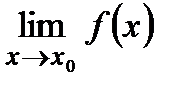 .
.
Если 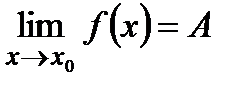 , то
, то 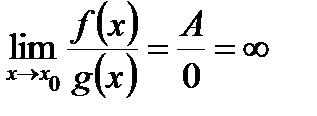 .
.
Если 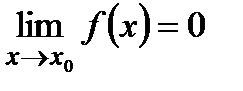 , то имеет место неопределенность
, то имеет место неопределенность 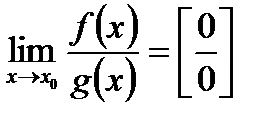 .
.
Для раскрытия неопределенности необходимо разложить числитель и знаменатель на множители, преобразовать дробь и воспользоваться теоремой предела частного. Для этого воспользуемся формулами сокращенного умножения:
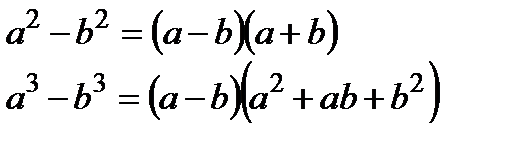
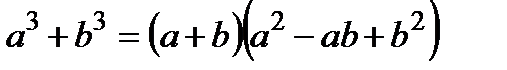
Разложить на множители квадратный многочлен типа 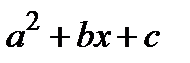 , можно найдя его корни, используя формулу дискриминанта
, можно найдя его корни, используя формулу дискриминанта 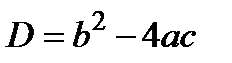 .
.
Тогда 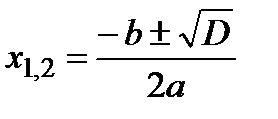 , а
, а 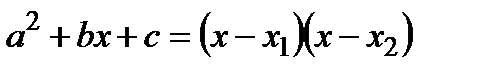 .
.
Если нельзя разложить на множители числитель и знаменатель, используется метод замены переменной. Заменим  на
на 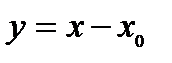 , при этом
, при этом 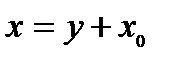 , а
, а 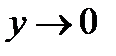 .
.
Далее используем теорему предела частного: 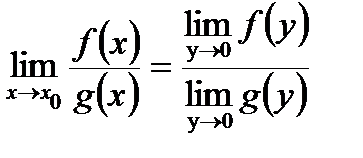 .
.
Пример: 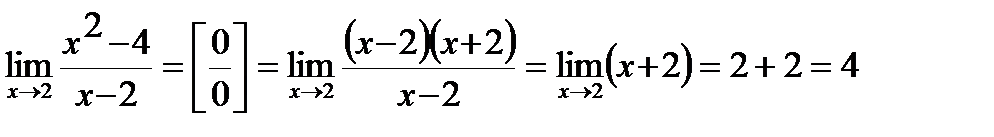
4.3 Предел частного на бесконечности
Для вычисления предела частного 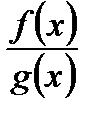 при
при 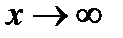 , необходимо числитель и знаменатель разделить на
, необходимо числитель и знаменатель разделить на  в максимальной степени и воспользоваться правилом
в максимальной степени и воспользоваться правилом 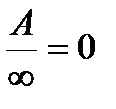 , чтобы раскрыть неопределенность
, чтобы раскрыть неопределенность 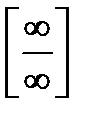 .
.
Пример: 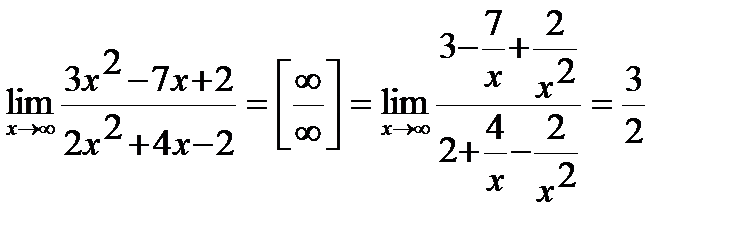
4.4 Предел иррациональных выражений
При вычислении пределов, содержащих иррациональные функции 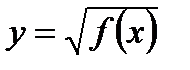 , необходимо умножить и числитель, и знаменатель на множитель, сопряженный с иррациональным.
, необходимо умножить и числитель, и знаменатель на множитель, сопряженный с иррациональным.
Далее воспользоваться правилом: 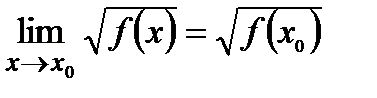 .
.
Пример: 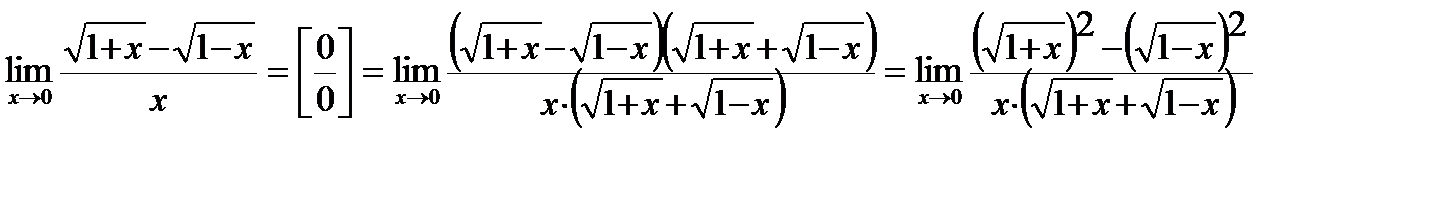
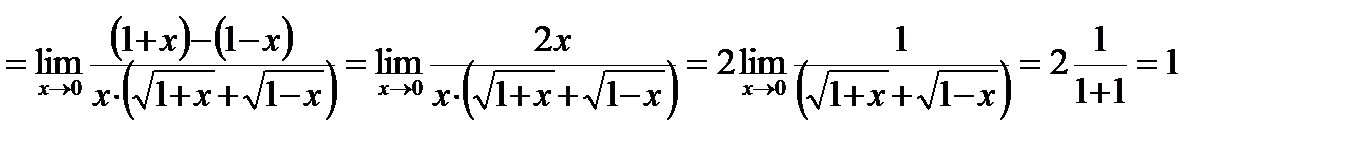
Поиск по сайту: