 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Понятие предела
Числовая последовательность – функция, определенная на множестве  натуральных чисел
натуральных чисел 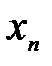 . Если множество значений ограничено – последовательность ограниченная. Такая последовательность может иметь предел. Пределом называют число, если существует точное
. Если множество значений ограничено – последовательность ограниченная. Такая последовательность может иметь предел. Пределом называют число, если существует точное  (номер члена последовательности) начиная с которого восполняется неравенство
(номер члена последовательности) начиная с которого восполняется неравенство 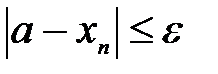 , где
, где 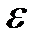 - сколько угодно малое положительное число. Обозначение:
- сколько угодно малое положительное число. Обозначение: 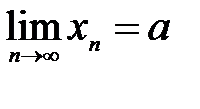
Рассмотрим простую линейную функцию 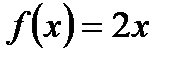 и зададимся вопросом, к какому числу А приближаются значения этой функции, когда значения переменной х приближаются к числу 3. Вычислим соответствующие значения f(x) и представим их в виде таблицы:
и зададимся вопросом, к какому числу А приближаются значения этой функции, когда значения переменной х приближаются к числу 3. Вычислим соответствующие значения f(x) и представим их в виде таблицы:
| х | 2,0 | 2,5 | 2,9 | 2,99 | 2,999 | 2,9999 |
| f(x) | 4,0 | 5,0 | 5,8 | 5,98 | 5,998 | 5,9998 |
| Х | 4,0 | 3,5 | 3,1 | 3,01 | 3,001 | 3,0001 |
| f(x) | 8,0 | 7,0 | 6,2 | 6,02 | 6,002 | 6,0002 |
Из таблицы видно, что значения функции f(x) приближаются к числу 6, если значения х приближаются к числу 3 как «слева» (по числовой прямой) так и «справа». Символически это записывается так: 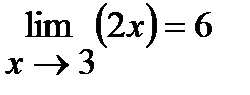 и читается: предел функции
и читается: предел функции 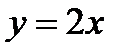 , когда х стремится к 3 (
, когда х стремится к 3 ( ), равен 6.
), равен 6.
Теперь дадим общее определение предела функции в точке.
Пусть функция y = f(x) определена в некоторой окрестности точки 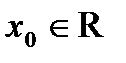 за исключением быть может, самой точки
за исключением быть может, самой точки  .
.
Определение1: Число А называется пределом функции y = f(x) при 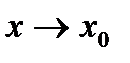 , если для любого
, если для любого 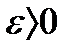 найдется
найдется 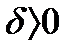 такое, что при всех х, удовлетворяющих неравенству
такое, что при всех х, удовлетворяющих неравенству  , будет выполняться неравенство
, будет выполняться неравенство  . Кратко это можно записать так:
. Кратко это можно записать так: 
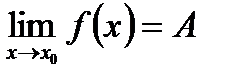
Выясним, что представляет собой геометрически понятие предела функции. Раскроем знаки модуля в неравенствах из определения предела функции: 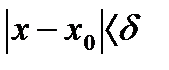 ,
, 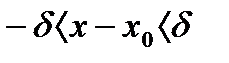 ,
,  Аналогично f(x)
Аналогично f(x) 
 .
.
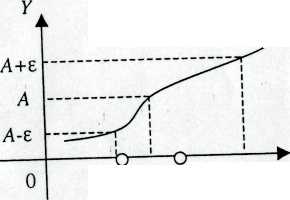
Геометрически это означает, что какую бы окрестность точки А на оси OY мы ни взяли, всегда найдется окрестность точки  на оси ОХ, которую функция переводит в окрестность оси OY.
на оси ОХ, которую функция переводит в окрестность оси OY.
 Х
Х
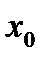 -
- 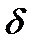
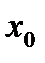
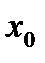 +
+ 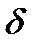
Дадим также определение предела функции на бесконечности и одностороннего предела.
Определение 2: Функция y=f(x) имеет предел на бесконечности при  , если для любого М>0 существует
, если для любого М>0 существует 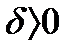 такое, что при всех х, удовлетворяющих неравенству
такое, что при всех х, удовлетворяющих неравенству  , будет выполняться неравенство f(x)>M (f(x)<-M).
, будет выполняться неравенство f(x)>M (f(x)<-M).
Кратко это можно записать так: 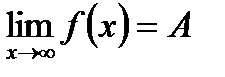
Определение 3: Число А называется пределом функции y=f(x) при при 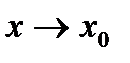 слева, или левосторонним пределом, если для любого
слева, или левосторонним пределом, если для любого 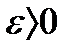 найдется
найдется 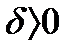 такое, что при всех х, удовлетворяющих неравенству
такое, что при всех х, удовлетворяющих неравенству 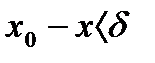 , будет выполняться неравенство
, будет выполняться неравенство  . Кратко это можно записать так:
. Кратко это можно записать так: 
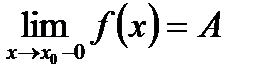
Определение 4: Число А называется пределом функции y=f(x) при 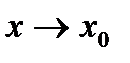 справа, или правосторонний пределом, если для любого
справа, или правосторонний пределом, если для любого 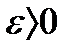 найдется
найдется 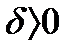 такое, что при всех х, удовлетворяющих неравенству
такое, что при всех х, удовлетворяющих неравенству 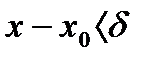 , будет выполняться неравенство
, будет выполняться неравенство  . Кратко это можно записать так:
. Кратко это можно записать так: 

Функция имеет предел в некоторой точке, равный некоторому значению, тогда и только тогда, когда существуют и равны этому же значению оба односторонних предела:
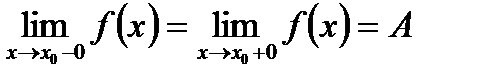
Рассмотрим функцию  , ее предел для любого
, ее предел для любого 

Рассмотрим функцию  , ее предел для любого
, ее предел для любого 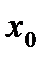

Пример: найти предел функции  при
при 
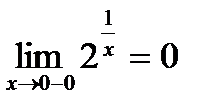 , т.к.
, т.к.  , то
, то 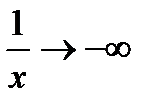 , а
, а 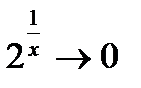
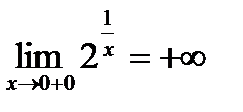 , т.к.
, т.к.  , то
, то  , а
, а 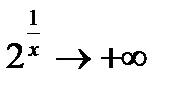
Таким образом, предел функции при х, стремящемся к нулю, не существует
Поиск по сайту: