Бесконечно большие и бесконечно малые функции

Определение 1: Функция 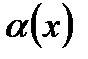называется бесконечно малой (б.м .) функцией при 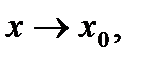если ее предел при 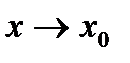равен нулю: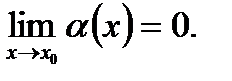

Определение 2: Функция 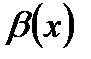называется бесконечно большой (б.б .) функцией при 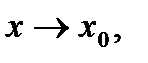если ее предел при 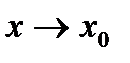равен :

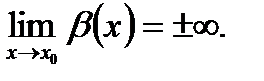
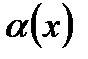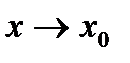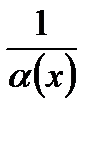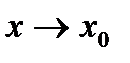
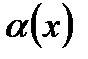Взаимосвязь бесконечно малых и бесконечно больших функций: если является бесконечно малой (б.м .) функцией при , то бесконечно большая при и наоборот если является бесконечно большой (б.б .) функцией при 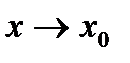, то бесконечно малая при .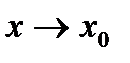

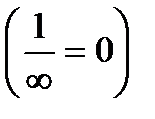Сравнение бесконечно малых функций.

Пусть функции 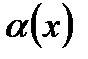и 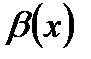бесконечно малые функции при 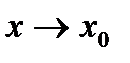. Предположим, что существует предел их отношения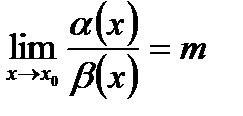

Тогда если: 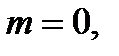то функция 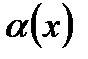бесконечно малая более высокого порядка, чем 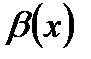, 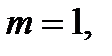то функци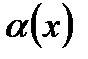и и 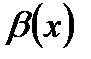эквивалентные бесконечно малые функции,

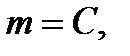то функци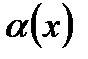и и 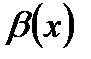бесконечно малые функции одинакового порядка,

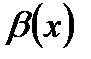то функция бесконечно малая более высокого порядка, чем .

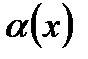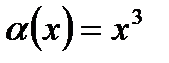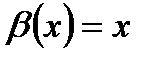Пример: Сравнить и при .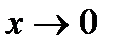

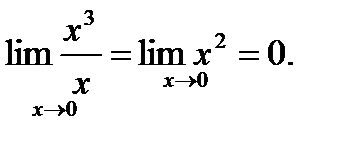
Таким образом, функция 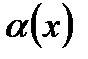более высокого порядка, чем .

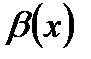Поиск по сайту: