АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Правило Лопиталя. Если функции f(x) и g(x) дифференцируемы в некоторой окрестно­сти точки , в некоторой окрестности точки и

Читайте также:
  1. Але монетарне правило не враховує мінливості швидкості обігу грошей та чутливості попиту до зміни процентної ставки.
  2. Виды светофоров и правило их установки
  3. Вопрос№10 Явление электромагнитной индукции. Правило Ленца
  4. Второе правило
  5. Глава VI. Правило фаз.
  6. Гондурасе, Панаме, Парагвае и, как правило, называются На-
  7. Доход и прибыль фирмы. Правило максимизации прибыли.
  8. Закон Фарадея для электромагнитной индукции. Правило Ленца.
  9. Законы Ньютона. Правило сложения сил.
  10. Заняття 14. Основні властивості та характеристики МП. Правило правохідного гвинта.
  11. Заняття 15. ЕМ сила. Правило лівої руки. Поняття про ДПС.
  12. Золотое правило поведения

Если функции f(x) и g(x) дифференцируемы в некоторой окрестно­сти точки , в некоторой окрестности точки и , то .

Правило Лопиталя распространяется на раскрытие не­определенностей вида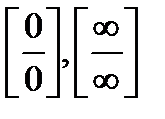

Пример: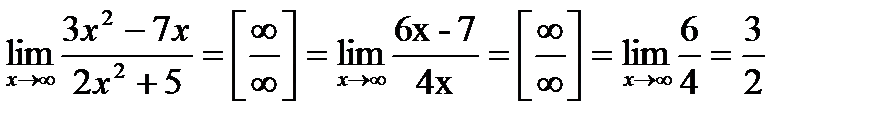

Контрольные вопросы:

1) Дайте определение производной функции?

2) Как называют операцию нахождения производной функции?

3) Сформулируйте общие правила дифференцирования функции и напишите формулы дифференцирования основных элементарных функций.

4) Как находится производная сложной функции?

5) Как найти производную неявной функции?

6) Что называют обратной функций?

7) Как находится производная обратной функции 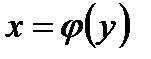для данной х=f(х), при каких условиях?

8) Дать понятие производных высшего порядка.

9) Что называют дифференциалом функции?

Задания для самостоятельной работы студентов:

1) Найти производную функции по определению: у=3х2-4х.

2) Используя таблицу производных найти производную сложной функции y=tg3 x2, , , , , .

3) Используя таблицу производных и правила дифференцирования найти производную , , , .

4) Найти производные высших порядков:

, , .

5) Найти дифференциал функции: , .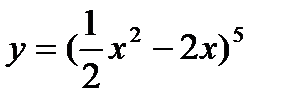


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)