Системы линейных уравнений. называется системой линейных уравнений с неизвестными, где

Система вида

(1.8)

называется системой линейных уравнений с неизвестными, где -неизвестные, , ,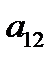…, - коэффициенты при неизвестных, , ,…, 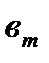-свободные члены.

Если свободные члены равны нулю, то система называется однородной, и неоднородной в противном случае.

Решениемсистемы называется совокупность чисел , которые, будучи подставлены вместо неизвестных в уравнения, обращают эти уравнения в тождества.

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если не имеет ни одного решения.

Совместная система называется определённой, если она имеет только одно решение, и неопределённой, если она имеет более одного решения.

При изучении систем исследуются три вопроса:

1) Совместна система или нет,

2) Если система совместна, то является ли она определенной или неопределенной,

3) Нахождение единственного решения в случае определенной системы и всех решений в случае неопределенной.

Поиск по сайту: