Дифференциал функции

Пусть функция y=f(x), дифференцируемая в некоторой точке интервала (а, в).

Если приращение функции можно представить в виде , где - б.м. функция более высокого порядка, чем при 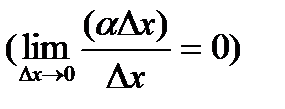, тогда .

Определение: Дифференциалом функции f(x) в точке называется линейная относительно 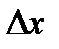величина , составляющая главную часть приращения функции f(x) в точке и обознача­ется dy=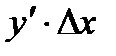

Теорема1. Функция не может иметь двух различных дифференциалов.

Теорема 2. Если функция дифференцируема в некоторой точке, то в этой точке она имеет дифференциал.

Теорема 3. Если функция имеет дифференциал в некоторой точке, то она имеет производную в этой точке.

Поиск по сайту: