АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Порядок решения задач на применение теоремы Гаусса к расчету напряженности электрического поля

Читайте также:
  1. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  2. I. Порядок медицинского отбора и направления на санаторно-курортное лечение взрослых больных (кроме больных туберкулезом)
  3. I. Решение логических задач средствами алгебры логики
  4. I. Розв’язати задачі
  5. I. Ситуационные задачи и тестовые задания.
  6. II Съезд Советов, его основные решения. Первые шаги новой государственной власти в России (октябрь 1917 - первая половина 1918 гг.)
  7. II. Основные задачи и функции
  8. II. Решение логических задач табличным способом
  9. II. ЦЕЛИ, ЗАДАЧИ И ПРИНЦИПЫ ДЕЯТЕЛЬНОСТИ ВОИ
  10. II. Цель и задачи государственной политики в области развития инновационной системы
  11. III Общий порядок перемещения товаров через таможенную границу Таможенного союза
  12. III. Решение логических задач с помощью рассуждений

1. Разобраться с симметрией заданного распределения зарядов и нарисовать картину силовых линий поля.

2. Выбрать поверхность интегрирования, учитывая симметрию задачи. Форма поверхности должна быть такой, чтобы силовые линии либо скользили по ее поверхности, либо были ей перпендикулярны. Разумный выбор поверхности интегрирования упрощает взятие интеграла при вычислении потока вектора напряженности через эту поверхность.

3. Найти поток вектора через выбранную поверхность.

4. Вычислить заряд, охватываемый этой поверхностью.

5. Подставить в теорему полученные выражения для потока вектора напряженности и суммарного заряда. Из полученного уравнения выразить искомую величину Е.

6. Если в задаче заданы численные значения величин, то, подставив их, получить численные значения напряженности поля для указанных точек.

7. Построить график зависимости величины напряженности поля от расстояния до заряда 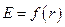, если это требуется по условию задачи.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)