АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Теорема Гаусса

Читайте также:
  1. S-M-N-теорема, приклади її використання
  2. Алгоритм решения систем линейных уравнений методом Жордана-Гаусса
  3. Вектор электрического смещения ( электрической индукции) D. Обобщение теоремы Гаусса для вещества.
  4. Внешние эффекты (экстерналии). Теорема Коуза.
  5. Внешние эффекты, их виды и последствия. Теорема Коуза
  6. Вопрос 1 теорема сложения вероятностей
  7. Вопрос 2 Нормальное распределение Гаусса
  8. Вопрос 24 Теорема Остроградского-Гаусса для электрического поля в вакууме
  9. Вопрос. Теорема Котельникова (Найквиста)
  10. Второй закон термодинамики. Энтропия. Закон возрастания энтропии. Теорема Нернста. Энтропия идеального газа.
  11. Гранична теорема Пуассона
  12. Дискретизація сигналу – теорема відліків (Котельникова)

В 1830 г. К. Гаусс сформулировал теорему (теорема Гаусса) – основную теорему электростатики, которая устанавливает связь между потоком вектора напряженности через произвольную замкнутую поверхность и суммарным электрическим зарядом, находящимся в объеме, ограниченном этой поверхностью.

Формулировка теоремы:

Поток вектора напряженности через произвольную замкнутую поверхность равен алгебраической сумме зарядов, охватываемых этой поверхностью, деленной на электрические постоянные ε,ε0.

,

где 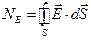- поток вектора напряженности через выбранную замкнутую вспомогательную поверхность; - суммарный заряд, охватываемый выбранной поверхностью. Если воле создано системой зарядов, то под суммой зарядов следует понимать алгебраическую сумму всех зарядов, охватываемых поверхностью :

.

В том случае, когда заряды распределены непрерывно, суммарный заряд вычисляется по одной из формул:

; ; ,

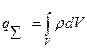где - - объемная плотность заряда; - поверхностная плотность заряда; - линейная плотность заряда; V, S, l - соответственно, объем, поверхность, линия, по которым распределены заряды, охватываемые поверхностью интегрирования.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)