АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Задачи для самостоятельного решения. Задача 3.1. Используя теорему Гаусса, найдите напряженность электрического поля равномерно заряженного эбонитового шара радиусом R = 20 см как функцию

Читайте также:
  1. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  2. I. Ситуационные задачи и тестовые задания.
  3. II Съезд Советов, его основные решения. Первые шаги новой государственной власти в России (октябрь 1917 - первая половина 1918 гг.)
  4. II. Основные задачи и функции
  5. II. ЦЕЛИ, ЗАДАЧИ И ПРИНЦИПЫ ДЕЯТЕЛЬНОСТИ ВОИ
  6. II. Цель и задачи государственной политики в области развития инновационной системы
  7. III. Цели и задачи социально-экономического развития Республики Карелия на среднесрочную перспективу (2012-2017 годы)
  8. VI. ДАЛЬНЕЙШИЕ ЗАДАЧИ И ПУТИ ИССЛЕДОВАНИЯ
  9. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
  10. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
  11. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА УРАВНЕНИЕ ТЕПЛОВОГО БАЛАНСА
  12. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ ПО ДИНАМИКЕ

Задача 3.1. Используя теорему Гаусса, найдите напряженность электрического поля равномерно заряженного эбонитового шара радиусом R = 20 см как функцию расстояния от центра шара 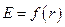, если объемная плотность заряда
r = 2 нКл/м3. Постройте график зависимости напряженности поля Е от расстояния r до центра шара от рассматриваемой точки. Диэлектрическая проницаемость эбонита .

Задача 3.2. Используя теорему Гаусса, найдите напряженность электрического поля равномерно заряженной полой сферической поверхности радиусом R = 15 см как функцию расстояния от центра сферы 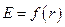, если полный заряд сферы q = 30 нКл.

Постройте график зависимости величины напряженности электрического поля Е от расстояния r до центра сферы.

Задача 3.3. Поле создается заряженной полой металлической сферой радиусом R = 15 см и точечным зарядом q = 10-9 Кл, расположенным в центре сферы. Величина поверхностной плотности заряда сферы s = 20 нКл/м2. Найдите зависимость напряженности поля внутри и вне сферы как функцию расстояния от центра сферы .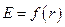

Постройте график зависимости напряженности поля от расстояния r до центра сферы.

Задача 3.4. Используя теорему Гаусса, найдите напряженность поля, создаваемого бесконечно протяженной заряженной нитью, как функцию расстояния r от нити. Линейная плотность заряда нити равна τ = 5.0 нКл/м. Постройте график зависимости E = f (r).

 

Задача 3.5. Используя теорему Гаусса, найдите напряженность поля, создаваемого тонкостенным бесконечно протяженным металлическим цилиндром радиуса R = 5.0 см, как функцию расстояния r от оси цилиндра. Поверхностная плотность заряда цилиндра равна σ = 10 нКл/м2. Постройте график зависимости E = f (r).

Задача 3.6. Поле создано зарядом бесконечного тонкостенного цилиндра радиусом R = 20 см и заряженной нитью с линейной плотностью заряда t = 5×10-9 Кл/м, расположенной вдоль оси цилиндра.

Пользуясь теоремой Гаусса, получите значение напряженности электрического поля внутри и вне цилиндра как функцию расстояния от центра цилиндра. Поверхностная плотность заряда цилиндра σ = 10-8 Кл/м2.

Построить график полученной зависимости .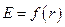

Задача 3.7. Используя теорему Гаусса, найдите напряженность поля, создаваемого сплошным металлическим шаром радиуса R = 10 см как функцию расстояния r от центра шара. Заряд шара равен q = 33 нКл. Постройте график зависимости E = f (r).

 

Задача 3.8. Используя теорему Гаусса, найдите напряженность поля, создаваемого заряженной бесконечно протяженной металлической плоскостью, как функцию расстояния х от плоскости. Поверхностная плотность заряда плоскости равна σ = 10 нКл/м2. Постройте график зависимости E = f (х).

 

Задача 3.9. Электростатическое поле создается двумя бесконечными пластинами, заряженными равномерно одноименными зарядами с поверхностной плотностью и .Используя теорему Гаусса и принцип суперпозиции электрических полей, найдите выражение для напряженности поля между пластинами и за пределами пластин. Постройте график зависимости E = f (х). Начало координат оси ОХ можно связать с любой пластиной и расположить эту ось перпендикулярно пластине.

 

 

Задача 3.10. Электростатическое поле создается двумя бесконечными пластинами, заряженными равномерно разноименными зарядами с поверхностной плотностью и .Используя теорему Гаусса и принцип суперпозиции электрических полей, найдите выражение для напряженности поля между пластинами и за пределами пластин. Постройте график зависимости E = f (х). Начало координат оси ОХ можно связать с любой пластиной и расположить эту ось перпендикулярно пластине.

3.4.1. Работа по перемещению заряда в электрическом поле. Потенциал. Разность потенциалов. Связь между напряженностью E и потенциалом j электрического поля.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)