 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Пример 3.2.3
Имеется длинный заряженный равномерно по объему цилиндр радиуса R 0 = 2 см, с e1 = 5. Плотность зарядов постоянна и равна r = 4 нКл/м3.
Найти напряженность поля в точках, расположенных на расстояниях r 1 = 1 см и r 2 = 3 см от оси цилиндра. Построить график зависимости Е (r).
r – радиальная координата.
Анализ и решение: 1. Необходимо нарисовать картину силовых линий заданного распределения зарядов.
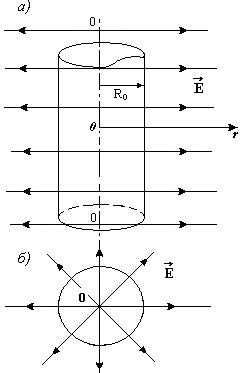Симметрия заданного распределения заряда позволяет считать, что поле обладает осевой симметрией, т.е. cиловые линии – радиальные прямые, перпендикулярные оси цилиндра. На рисунках показаны силовые линии поля цилиндра: а) ход силовых линий показан в плоскости сечения, проходящей через ось цилиндра; б) ход силовых линий показан в плоскости сечения, перпендикулярной оси цилиндра.
2. Выбирем поверхность интегрирования, учитывая симметрию задачи, таким образом, чтобы силовые линии поля либо скользили по поверхности, либо были ей перпендикулярны.
Замкнутую поверхность для нахождения потока в случае радиально симметричного поля удобно выбрать в виде цилиндра, ось которого совпадает с осью заряженного тела; высота цилиндра выбирается произвольно.
При решении нашей задачи надо найти напряженность в двух случаях: а) когда r < R 0; б) когда r > R 0.
Поверхности для этих случаев изображены на рисунках пунктирной линией. Они отличаются радиусами. Каждый раз радиус поверхности интегрирования равен расстоянию от оси до точки, в которой находится поле.
3. Вычислим поток вектора 
через выбранную поверхность.
Полный поток 
через замкнутую поверхность можно представить как сумму потоков через два основания цилиндра и через его боковую поверхность
.
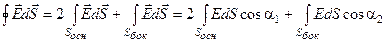Как видно из рисунка, a1 =900, а a2 = 00, следовательно, поток отличен от нуля только для боковой поверхности.
С учетом этого получим
.
Перед первым интегралом стоит множитель «2», т.к. два основания симметрично расположены и модуль вектора Е на равных расстояниях от пластины будет одинаков во всех точках оснований и в данном случае будет равен нулю.
Модуль вектора Е на равных расстояниях от оси цилиндра будет иметь одинаковые значения и поэтому при вычислении потока вектора Е через боковую поверхность цилиндра его можно вынести за знак интеграла
.
4. Запишем выражение для заряда, охватываемого поверхностью интегрирования.
.
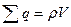а) Интересующая нас точка находится внутри заряженного цилиндра, поэтому выбранная поверхность охватывает заряд, находящийся внутри цилиндра радиусом r и высотой h:
.
б) Интересующая нас точка находится внt заряженного цилиндра, поэтому выбранная поверхность интегрирования охватывает заряд, находящийся внутри цилиндра радиуса R 0, т.к. заряд находится только внутри цилиндра радиуса R 0, а дальше его нет и высотой h:
,
5. Воспользуемся теоремой Гаусса:
Подставим выражения, полученные в пунктах 3 и 4 в левую и правую части теоремы Гаусса. Из полученного уравнения, выразим Е. Получаем:
.
а) Для точек, лежащих внутри цилиндра, получаем:
;
где e1 – диэлектрическая проницаемость материала заряженного цилиндра, по условию e1 = 5;
Отсюда получаем формулу зависимости напряженности поля заряженного цилиндра для точек, лежащих внутри цилиндра
;
Для точки, находящейся на расстоянии r 1 = 1 см от оси цилиндра напряженность поля равна:
.
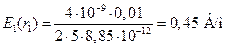б) Для точек, лежащих вне цилиндра, запишем уравнение
;
Из которого получим формулу для вычисления напряженности поля для точек, лежащих вне цилиндра:
;
где e2 - диэлектрическая проницаемость среды, окружающей заряженный цилиндр, e2 = 1 т.к. цилиндр находится в воздухе.
Для точки, находящейся на расстоянии r 2 = 3 см от оси цилиндра напряженность поля равна:
.
Построим график зависимости E = f (r).
Внутри цилиндра радиуса R0 зависимость Е от r имеет вид
, где r – любое расстояние меньшее R 0, т.е. зависимость линейная и график – прямая линия.
Вне цилиндра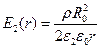 
, где r – расстояние, большее R 0, величина Е обратно пропорциональна расстоянию r до оси цилиндра, следовательно, график представляет собой гиперболу.
При переходе из цилиндра в воздух Е скачком возрастает из-за изменения диэлектрической проницаемости среды.
Поиск по сайту: