Пример 3.3.3

Электрическое поле образовано положительно заряженной бесконечно длинной нитью с линейной плотностью заряда t = 0,2 мк Кл/м. Какую скорость V будет иметь покоящийся электрон, если он под действием сил поля, приблизится к нити с расстояния r ₁ = 1 см до расстояния r ₂ = 0,5 см.

Дано:

t = 0,2 мк Кл/м = 2×10^-7 Кл/м;

r ₁ = 1 см = 0,01 м;

r ₂ = 0,5 см = 5×10^{-3 м;}

m _e = 9,1×10^{-31 кг;}

V _{0 =} 0

_ е _=1,610^-19Кл_

___________

V -?

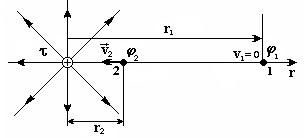
Анализ и решение: На рисунке показаны силовые линии поля нити в плоскости, перпендикулярной самой нити, и радиальная ось.

Для описания поведения заряженной частицы в электростатическом поле можно применить закон сохранения энергии, т.к. система замкнута и консервативна.

При движении отрицательной частицы силы поля будут совершать положительную работу, и это приведет к тому, что потенциальная энергия заряда будет убывать, а кинетическая возрастать.

В первой точке электрон имеет только потенциальную энергию, поскольку в начальный момент он покоился,

W _к1 = 0, W _п1 = e j_1.

Во второй точке у заряда будет и потенциальная и кинетическая энергия

W _п2 = e j₂.

По закону сохранения энергии

W _к1 + W _п1 = W _к2 + W _п2

или

;

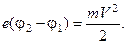
Для нахождения (j₂ - j₁) воспользуемся формулой, связывающей E с потенциалом j. Для случая радиальной симметрии

или

Напряженность поля нити нам известна: , для воздуха e = 1, с учетом этого, получаем

Проинтегрируем это уравнение по координате r

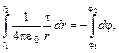
вынесем постоянные множители из-под интеграла и получим

Используя табличные интегралы, получим

,

или

Подставляя полученное уравнение в выражение закона сохранения энергии, получим

-

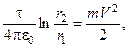
отсюда

Подставляя численные значения, получаем

Ответ: электрон приобретет скорость, равную V = 2,97×10⁷ м/с.

Пример 3. 1 Две длинные одноимённо заряженные нити расположены на расстоянии r ₁= 10см друг от друга. Линейные плотности зарядов одинаковы и равны = =10мкКл/м.

Какую работу А на единицу длины нити надо совершить, чтобы раздвинуть нити до расстояния 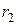= 20см?

Анализ:

Дано:
r	=10см =20см =10мкКл/м
r2
=
a	=10см
1) E -? 2) A -?

Электростатические поля, создаваемые различными распределениями зарядов, по принципу суперпозиции складываются в каждой точке пространства. Учитывая симметрию задачи, сделаем рисунок, расположив нити перпендикулярно плоскости чертежа. Точка А удалена от обеих нитей на расстояние а = r ₁.Получили равносторонний треугольник. Для того, чтобы найти направление вектора напряжённости поля, создаваемого в точке А зарядом каждой нити, поместим в эту точку пробный заряд «+1» и определим, как поля нитей действуют на этот заряд. Так как нити заряжены положительно, то они будут отталкивать пробный заряд и вектора и будут направлены так, как показано на рисунке. Вектор напряжённости суммарного поля, согласно принципу суперпозиции, находится по правилу параллелограмма.

Сила взаимодействия этих заряженных нитей зависит от расстояния между ними, поэтому работу сил электростатического поля при раздвижении нитей надо вычислять через интеграл.

Решение:

1) Из рисунка видно, что направлен вправо, и модуль его можно найти как:

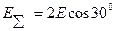
т.к. 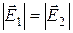и , где k= .

Окончательно получаем

.

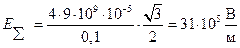2) Сила взаимодействия заряженных нитей зависит от расстояния между ними. Каждая нить создаёт поле, и это поле действует на заряд другой нити. - напряженность поля первой нити.

-сила, действующая на единицу длины второй нити равна:

Работу этой силы можно вычислить как:

.

Возьмём интеграл от этой функции. Все постоянные величины выносим за знак интеграла и получаем табличный интеграл, который равняется натуральному логарифму аргумента.

Подставим пределы интегрирования и окончательно получаем:

.

Используя данные задачи, получим численный ответ

Ответ: 1) 2)

Поиск по сайту: