 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Примеры решения задач. Пример 3. Площадь пластин плоского воздушного конденсатора S = 0,01 м2, расстояние между ними d = 5 мм
Пример 3. Площадь пластин плоского воздушного конденсатора S = 0,01 м2, расстояние между ними d = 5 мм. К пластинам приложена разность потенциалов U 1 = 300 B. После отключения конденсаторов от источника напряжения пространство между пластинами заполняется эбонитом. Какова будет разность потенциалов U 2 между пластинами после заполнения? Найти емкости конденсатора С 1 и С 2 и поверхностные плотности заряда s1 и s2 на пластинах до и после заполнения. Диэлектрическая проницаемость эбонита e = 2,6.
Дано:
S = 0,01 м2
d = 5 мм = 0,005 м;
U 1 = 300 В;
e = 2,6
___________
C 1 -? C 2 -? Анализ: Конденсатор заполняют эбонитом при
s1 -? s2 -? U 2 -? отключенном источнике, следовательно, заряд не изменяется q 1 = q 2. Поверхностная плотность зарядов также не изменяется: 
Емкость плоского конденсатора зависит прямо пропорционально от диэлектрической проницаемости среды между обкладками конденсатора 
, поэтому при внесении эбонита в пространство между обкладками, емкость конденсатора увеличивается в раз.
Решение: Определим емкости конденсатора до и после внесения диэлектрика.
Емкость конденсатора можно вычислить по формуле 
.
В первом случае среда между обкладками - воздух, т.е. e1 = 1, а во втором - эбонит (e2 = 2,6).
Подставив численные значения, получаем:
Для определения разности потенциалов после внесения диэлектрика в конденсатор воспользуемся формулами для вычисления напряженности поля плоского конденсатора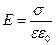 
и формулой, связывающей напряженность поля с разностью потенциалов 
До внесения диэлектрика среда между обкладками – воздух, следовательно, e1 = 1 и поэтому 
и 
После внесения эбонита диэлектрическая проницаемость станет равной e2 = 2,6.
Учитывая это, можно написать 
и 
Сравнивая эти формулы, получаем 
Подставив численные значения, получаем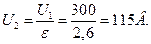 
Осталось определить поверхностную плотность заряда на обкладках конденсатора. Мы уже отмечали, что заряд на конденсаторе не изменяется, т.к. источник питания отключен, поэтому определим величину s1 из формулы для разности потенциалов в первом случае
или 
Вычислим численное значение поверхностной плотности заряда
Ответ: после заполнения конденсатора эбонитом установилось напряжение, равное 115 В, емкости конденсатора до и после заполнения соответственно равны 17,7пФ и 46 пФ, поверхностные плотности заряда будут одинаковы и равны 531 нКл/м.
Поиск по сайту: