 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Теорема Гаусса. Применение теоремы Гаусса к расчету напряженности электрического поля
Расчет электрического поля, основанный на непосредственном применении закона Кулона и принципа суперпозиции, достаточно несложный в случае небольшого количества зарядов или очень простой геометрии заряженных тел. В более сложных случаях применение непосредственно принципа суперпозиции приводит к громоздким математическим выкладкам. Существует несколько методов облегчения решения таких задач. Один из них основан на теореме Гаусса.
Поток вектора напряженности. Прежде, чем формулировать теорему Гаусса, рассмотрим понятие потока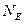 
вектора напряженности 
через некоторую площадку 
. По определению:
Поток вектора напряженности электрического поля через некоторую площадь равняется скалярному произведению этих векторов:
,
где - вектор напряженности электрического поля; 
- вектор, численно равный площади, через которую проходит поток вектора ; направление этого вектора совпадает с направлением единичного вектора 
, перпендикулярного к этой площадке. α - угол между вектором и единичным вектором .
В случае однородного поля угол α является постоянным (см. рис. а).
В случае неоднородных полей поток вектора напряженности через произвольную поверхность вычисляется следующим образом с помощью интегрирования:
, если поверхность замкнутая, то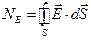 
.
Элементарная площадка должна быть достаточно малой, чтобы ее можно было считать плоской, а напряженность поля во всех ее точках одинаковой (см. рис. б).
Поток вектора - алгебраическая скалярная величина, ее знак зависит от выбора направления нормали к элементарным площадкам, т. е. от угла между вектором и нормалью . В теореме Гаусса речь идет о замкнутых поверхностях, поэтому договоримся под нормалью к поверхности считать внешнюю нормаль, т.е. нормаль обращенную наружу.
Для более наглядной геометрической интерпретации этой физической величины можно дать еще такое ее определение: поток вектора это число силовых линий вектора напряженности электрического поля, пронизывающих данную площадь S.
Поиск по сайту: