Примеры решения задач на закон Кулона

Пример 1. Два одинаковых по размеру маленьких металлических шарика имеют заряды q₁ = 7мкКл и q₂ = - 3 мкКл. Шарики привели в соприкосновение и развели на некоторое расстояние. Определите это расстояние r (в см.), если сила взаимодействия зарядов при этом оказалась равной F = 40 Н.

Дано:

q₁=7 мкКл

q₂=-3 мкКл

F = 40 Н

Найти:

r=?

Анализ: Маленькие заряженные шарики можно считать точечными зарядами.

Система шаров является электроизолированной и для нее выполняется закон сохранения заряда. При приведении их в соприкосновение происходит перераспределение суммарного заряда. Поскольку размеры шариков одинаковые, то суммарный заряд системы поделится между ними поровну. Рисунок в этой задаче необязателен, т.к. при написании уравнений, из которых мы будем находить искомую величину, направления сил неважны. Нам в условии задан модуль силы взаимодействия зарядов после их соприкосновения.

Решение: Закон сохранения заряда: в любой электроизолированной системе алгебраическая сумма электрических зарядов остается величиной постоянной.

В нашем случае .

Отсюда заряд каждого шарика после их соприкосновения равен: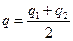

Записав закон Кулона в конечном положении

,

Определим расстояние между зарядами в конечном состоянии:

.

Выполним подстановку численных значений

.

Ответ: .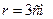

Пример 2. Два одинаковых по размеру маленьких металлических шарика висят на длинных непроводящих нитях равной длины, закрепленных в одной точке. Шарики заряжены одинаковыми зарядами и находятся на расстоянии друг от друга. Что произойдет, если один из шариков разрядить?

Дано:

Найти:

Анализ: Два одинаковых шарика, заряженные одинаковыми одноименными зарядами, висят на длинных непроводящих нитях равной длины, закрепленных в одной точке, и сохраняют равновесие (см. рис. а). На каждый шарик при этом действуют три силы: сила тяжести , сила натяжения нити и сила кулоновского отталкивания , поскольку заряды шариков одноименные. После того как один шарик разрядили, равновесие нарушится, шарики столкнуться и при этом оставшийся заряд одного шарика поделится между ними поровну, т.к. шарики имеют одинаковые размеры. Зарядившись опять одноименными зарядами, они оттолкнутся и равновесие восстановится, но расстояние между шариками изменится, станет равным (см. рис. б), т.к. все силы, действующие на шарики, изменятся.

Решение: Выполним рисунок к данной задаче. Покажем два случая: (а) - положения 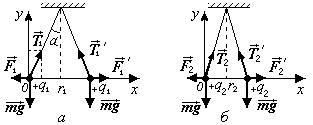шариков в начальный момент; (б) – положения шариков после изменения их зарядов. Из рисунка видно, что система симметрична относительно вертикальной линии, проходящей через точку прикрепления нитей, поэтому для решения задачи достаточно рассмотреть поведение одного из шариков и записать для него условия равновесия. Если тело не движется поступательно, то для него можно записать следующее условие равновесия: векторная сумма сил, действующих на тело равна нулю, т.е. . Проектируя это уравнение на оси координат декартовой системы, выбор которой показан на рисунке, получаем два уравнения

или

или

Эта система уравнений будет иметь одинаковый вид для первого и второго случаев, поэтому сначала найдем решение этой системы уравнений в общем случае, а потом применим полученный результат для нахождения искомой величины в нашем конкретном случае. По условию задачи нить длинная, т.е. и поэтому . Поделив правую часть первого уравнения на правую часть второго уравнения и соответственно поделив левые части уравнений, получим

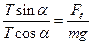или .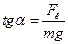

Величину силы взаимодействия зарядов запишем, используя закон Кулона:

.

Для малых углов 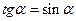величина малая, но неравная нулю. Из рисунка видно, что .

Подставим выражения для силы Кулона и тангенса угла α, получим уравнение из которого можно выразить расстояние между зарядами в общем случае

или .

Теперь вернемся к условию нашей задачи. В первом случае каждый шарик имеет заряд и расстояние между ними . В о втором случае один шарик разрядили, а заряд второго разделился поровну между двумя шариками, поэтому их заряды во втором случае будут одинаковые и равные ; расстояние между ними будет . Учитывая все это, можно записать полученное уравнение для двух случаев:

и .

Решая эту систему уравнений, получаем

, отсюда находим искомое расстояние между зарядами во втором случае . Подставив численные значения,

Получаем

Ответ: После разрядки одного из шариков заряд второго шарик при их соударении поровну разделится между ними и оттолкнувшись шарики разойдутся на расстояние .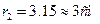

Поиск по сайту: