Потенциал. Разность потенциалов

Электростатическое поле является потенциальным полем, поэтому заряды, находящиеся в поле обладают энергией. Энергия единичного положительного заряда может служить энергетической характеристикой электрического поля.

Потенциал электростатического поля – скалярная физическая величина, являющаяся энергетической характеристикой поля в данной точке и равная энергии единичного положительного заряда, помещенного в данную точку поля:

.

Отсюда следует, что энергия любого точечного заряда, помещенного в точку с потенциалом 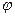, равна .

Если силы консервативны, то их работа равна убыли потенциальной энергии тела. Электростатические силы являются консервативными силами и поэтому их работа равна убыли потенциальной энергии перемещаемого заряда

или ;

Таким образом, работа сил электростатического поля по перемещению заряда, равна произведению величины этого заряда на разность потенциалов начальной и конечной точек пути.

Потенциал, как и потенциальная энергия, определяется с точностью до произвольной постоянной, зависящей от выбора нулевого потенциального уровня.

При перемещении положительного заряда из данной точки, с потенциалом 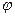в точку с нулевым потенциалом, силы поля совершат работу

откуда следует, что .

Можно дать еще одно определение потенциала:

Потенциал данной точки поля относительно некоторого нулевого уровня численно равен работе, совершаемой силами электростатического поля при перемещении единичного положительного заряда из данной точки поля на нулевой уровень.

Потенциал - величина алгебраическая. Знак потенциала определяется знаком заряда, создающего поле.

Для потенциала выполняется принцип суперпозиции: потенциал поля, создаваемого системой зарядов в данной точке равен алгебраической сумме потенциалов, создаваемых в этой точке отдельными зарядами.

Для системы точечных зарядов потенциал результирующего поля равен

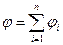
Если поле создается непрерывным распределением заряда, то потенциал равен

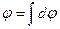
Для наглядного представления о распределении электрического поля вокруг заряда используется не только линии вектора напряженности, но и эквипотенциальные поверхности. Эквипотенциальная поверхность - поверхность равного потенциала или поверхность, во всех точках которой потенциал имеет одинаковое значение. Сечение эквипотенциальных поверхностей на рисунках изображают штрих пунктирной линией.

Что надо помнить об эквипотенциальных поверхностях

1) Эквипотенциальная поверхность расположена перпендикулярно вектору напряженности поля в каждой точке.

2) Работа электростатических сил по перемещению заряда между любыми двумя точками поверхности всегда равна нулю.

Связь между напряженностью E и потенциалом j электрического поля.

Для количественной характеристики электрического поля имеется две величины: напряженность поля – это силовая характеристика поля и потенциал – энергетическая характеристика поля. Найдем связь между этими величинами.

Работа по перемещению точеного положительного заряда на бесконечно малое расстояние dх равна

С другой стороны та же работа равна

.

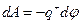Приравняв правые части этих уравнений, получаем

.

Если перемещение заряда происходит в трехмерном пространстве, и имеются перемещения по всем трем пространственным осям, то получим следующие соотношения:

, , ,

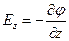тогда вектор напряженности поля можно выразить следующим образом

,

где , , - единичные векторы (орты) координатных осей ОХ, ОУ, ОZ;

, , - частные производные от потенциала по координатам х, у, z.

Оператор называется градиентом и обозначается grad или .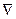

Градиентом скалярной величины называется вектор, направленный в сторону наиболее быстрого возрастания величины и численно равный приращению величины на единицу длины данного направления.

Для напряженности получили , т.е. напряженность поля равна градиенту потенциала со знаком минус. Знак «минус» отражает тот факт, что вектор напряженности всегда направлен в сторону убыли потенциала.

Поиск по сайту: