АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Условия максимума и минимума интерференции света через разность фаз и оптическую разность хода

Читайте также:
  1. I. При каких условиях эта психологическая информация может стать психодиагностической?
  2. I. Психологические условия эффективности боевой подготовки.
  3. III Общий порядок перемещения товаров через таможенную границу Таможенного союза
  4. IV. ТРЕБОВАНИЯ К УЧАСТНИКАМ И ИХ УСЛОВИЯ ДОПУСКА
  5. V. ОСНОВНАЯ ПРАКТИКА ЯСНОГО СВЕТА
  6. VI ПРИЧИНЫ, УСЛОВИЯ И ВТОРЖЕНИЕ
  7. А) ОСНОВНЫЕ УСЛОВИЯ ВЕРНОЙ ПЕРЕДАЧИ СЛОВ, ОБОЗНАЧАЮЩИХ НАЦИОНАЛЬНО-СПЕЦИФИЧЕСКИЕ РЕАЛИИ
  8. А) плечевой пояс проходит через грудную клетку; б) характерны анальные пузыри; в) зубы преобразовались в роговые пластины; г) уплощенные и широкие ребра.
  9. А) Спектр света и значение разного типа излучений
  10. А. Стекание тока в землю через одиночные заземлители
  11. АДАПТАЦИЯ И ОСНОВНЫЕ СПОСОБЫ ПРИСПОСОБЛЕНИЯ ЖИВЫХ ОРГАНИЗМОВ К ЭКСТРЕМАЛЬНЫМ УСЛОВИЯМ СРЕДЫ
  12. Алг «нахождение минимума»

Интерференцией волн называется явление усиления колебаний в одних точках пространства и ослабления колебаний в других точках в результате наложения двух или более волн, приходящих в эти точки. При наложении двух (или нескольких) световых волн происходит пространственное перераспределение светового потока, в результате чего в одних местах возникают максимумы, а в других – мини­мумы интенсивности. Необходимым условием наблюдения устойчивой интерференционной картины является когерентность складываемых волн. Когерентными называются волны одинаковой частоты, колебания в которых отличаются постоянной во времени разностью фаз.

Для получения когерентных световых волн применяют метод разделения волны, излучаемой одним источником, на две части, которые после прохождения разных оптических путей накладываются друг на друга, и в результате наблюдается интерференци­онная картина.

Произведение геомет­рической длины s пути световой волны в данной среде на показатель n преломления этой среды называется оптической длиной пути L, a величина D = L 2 – L 1 (разность оптических длин проходимых волнами путей) называется оптической разностью хода.

Если оптическая разность хода D равна целому числу длин волн l 0, т.е. ( = 0, 1, 2,…), то колебания, возбуждаемые в точке М обеими волнами, будут проис­ходить в одинаковой фазе, и в точке М будет наблюдаться интерференционный максимум (m – порядок интерференционного максимума).

Если же оптическая разность хода D равна полуцелому числу длин волн l 0, т.е. 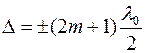( 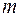= 0, 1, 2,…),

то колебания, возбуждаемые в точке М обеими волнами, будут проис­ходить в противофазе, и в точке М будет наблюдаться интерференционный минимум (m – порядок интерференционного минимума).

 

 

12. Работа по перемещению заряда в электростатическом поле. Теорема о циркуляции вектора напряженности. Потенциал.

Однородное электростатическое поле: в каждой точке поля.

. Следовательно: Т.к. если вектор перемещения перпендикулярен вектору силы (напряженности поля), работа поля равна нулю, то работа электростатического поля по перемещению заряда по любой траектории определяется разностью координат этих точек. Если обозначить координаты заряда в начальной и последующей точках r1 и r2, то:

Т.е. работа равна разности двух эквивалентных величин, зависящих от характера взаимодействия и взаимного расположения. Но мы знаем, что работа - мера изменения энергии. Можно предположить: W=qEr - потенциальная энергия заряда в данной точке электростатического поля. Зависит от выбора начальной точки отсчета потенциальной энергии. Тогда: - наиболее общий способ расчета работы в электростатическом поле. Т. е. работа при перемещении заряда между двумя точками в электростати­ческом поле

Рассмотрим перемещение заряда q в электростатическом поле по замкнутой траектории (рис. 3.5.). Заряд из точки 1 перемещается по пути L1 в точку 2, а затем возвращается в исходное положение по другому пути L2. В процессе этого движения на заряд со стороны поля действует консервативная электрическая сила:

. Работа этой силы на замкнутой траектории L = L1 + L2 равна нулю: . Это уравнение, упростив, запишем так: .

Подынтегральное выражение — элементарная работа электрической силы, действующей на единичный положительный заряд, на перемещении :

, (3.19), здесь q = 1 — единичный заряд.

При подсчёте работы на замкнутой траектории необходимо сложить элементарные работы электрической силы на всех участках траектории. Иными словами, проинтегрировать (3.19) по замкнутому контуру L: .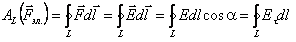

Интеграл по замкнутому контуру = 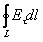называется циркуляцией вектора напряжённости электростатического поля по контуру L. По своей сути циркуляция вектора напряжённости — это работа электростатического поля, совершаемая при перемещении по замкнутому контуру единичного положительного заряда.

Так как речь идёт о работе консервативной силы, то на замкнутой траектории она равна нулю: .

Теорема о циркуляции в электростатике: циркуляция вектора напряжённости электростатического поля по любому замкнутому контуру равна нулю.

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)