Дифракция: принцип Гюйгенса – Френеля. Метод зон Френеля. Дифракция на щели

Принцип Гюйгенса является развитием принципа, который ввёл Гюйгенс: каждая точка фронта (поверхности, достигнутой волной) является вторичным (т.е. новым) источником сферических волн. Огибающая фронтов волн всех вторичных источников становится фронтом волны в следующий момент времени.

Принцип Гюйгенса объясняет распространение волн, согласующееся с законами геометрической оптики, но не может объяснить явлений дифракции. Френель дополнил принцип Гюйгенса, введя представления о когерентности и интерференции элементарных волн, что позволило рассматривать на основе принципа Гюйгенса — Френеля и дифракционные явления.

Принцип Гюйгенса — Френеля формулируется следующим образом:

Каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

Фронтом волны точечного источника в однородном изотропном пространстве является сфера. Амплитуда возмущения во всех точках сферического фронта волны, распространяющейся от точечного источника, одинакова.

Дальнейшим обобщением и развитием принципа Гюйгенса является формулировка через интегралы по траекториям, служащая основой современной квантовой механики.

Френель предложил оригинальный метод разбиения волновой поверхности S на зоны, позволивший сильно упростить решение задач (метод зон Френеля).

Границей первой (центральной) зоны служат точки поверхности S, находящиеся на расстоянии 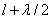от точки M. Точки сферы S, находящиеся на расстояниях , , и т.д. от точки M, образуют 2, 3 и т.д. зоны Френеля.

Колебания, возбуждаемые в точке M между двумя соседними зонами, противоположны по фазе, так как разность хода от этих зон до точки M .

Поэтому при сложении этих колебаний, они должны взаимно ослаблять друг друга:

, (9.2.2)

где A – амплитуда результирующего колебания, – амплитуда колебаний, возбуждаемая i -й зоной Френеля.

Величина зависит от площади зоны и угла между нормалью к поверхности и прямой, направленной в точку M.

Площадь одной зоны .

Отсюда видно, что площадь зоны Френеля не зависит от номера зоны i. Это значит, что при не слишком больших i площади соседних зон одинаковы.

В то же время с увеличением номера зоны возрастает угол и, следовательно, уменьшается интенсивность излучения зоны в направлении точки M, т.е. уменьшается амплитуда . Она уменьшается также из-за увеличения расстояния до точки M: .

Общее число зон Френеля, умещающихся на части сферы, обращенной в сторону точки M, очень велико: при , , число зон , а радиус первой зоны .

Отсюда следует, что углы между нормалью к зоне и направлением на точку M у соседних зон примерно равны, т.е. что амплитуды волн, приходящих в точку M от соседних зон, примерно равны.

Световая волна распространяется прямолинейно. Фазы колебаний, возбуждаемые соседними зонами, отличаются на π. Поэтому в качестве допустимого приближения можно считать, что амплитуда колебания от некоторой m -й зоны равна среднему арифметическому от амплитуд примыкающих к ней зон, т.е. .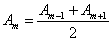

Тогда выражение (9.2.1) можно записать в виде

.

Так как площади соседних зон одинаковы, то выражения в скобках равны нулю, значит результирующая амплитуда .

Интенсивность излучения .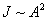

Таким образом, результирующая амплитуда, создаваемая в некоторой точке M всей сферической поверхностью, равна половине амплитуды, создаваемой одной лишь центральной зоной, а интенсивность .

Так как радиус центральной зоны мал (), следовательно, можно считать, что свет от точки P до точки M распространяется прямолинейно.

Если на пути волны поставить непрозрачный экран с отверстием, оставляющим открытой только центральную зону Френеля, то амплитуда в точке M будет равна . Соответственно, интенсивность в точке M будет в 4 раза больше, чем при отсутствии экрана (т.к. ). Интенсивность света увеличивается, если закрыть все четные зоны.

Таким образом, принцип Гюйгенса–Френеля позволяет объяснить прямолинейное распространение света в однородной среде.

Правомерность деления волнового фронта на зоны Френеля подтверждена экспериментально. Для этого используются зонные пластинки – система чередующихся прозрачных и непрозрачных колец.

Опыт подтверждает, что с помощью зонных пластинок можно увеличить освещенность в точке М, подобно собирающей линзе.

Поиск по сайту: