 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Пример 3.1
Найти напряженность 
электрического поля в точках А и В
(см. рис.), лежащих на серединном перпендикуляре между точечными зарядами q 1 = 8 нКл и q 2 = –6 нКл, находящимися в вакууме. Расстояние между зарядами r = 10 см, АВ = 4 см, e = 1. 
Дано:
q 1 = 8 нКл;
q 2 = -6 нКл;
r = 10 см;
AB = 4 см;
e = 1
Е А -?
Е В -?
Анализ и решение:
На рисунке показано расположение зарядов и точек А и В, для которых надо найти напряженность поля, и показан выбор системы координат.
а) В точке А поле создается двумя точечными зарядами q 1 и q 2. По определению напряженность поля - это сила с которой заряд, создающий поле, действует на единичный положительный точечный заряд, помещенный в точку А, поэтому вектора напряженностей 
и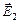 
в этой точке направлены в одну сторону. Суммарная напряженность находится как сумма напряжённостей полей отдельных зарядов
,
или в проекции на ось ОХ
.
Запишем формулы для вычисления модулей векторов напряженностей поля точечных зарядов q 1 и q 2 в точке А:
и 
.
Для точки А получаем:
.
б). В точке В векторы 
и 
направлены под углом 2a друг к другу и модули этих векторов не одинаковые, т.к. величины зарядов q 1 и q 2 разные.
Запишем формулы для вычисления модулей векторов напряженностей поля точечных зарядов q 1 и q 2 в точке В:
и 
.
Каждый из этих векторов дает проекцию на обе координатные оси:
, 
, 
, 
.
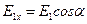Проекции суммарного вектора напряженности в точке В будут равны:
и 
.
Теперь по теореме Пифагора можно получить формулу для вычисления модуля вектора напряженности электрического поля, создаваемого в точке В зарядами q 1 и q 2.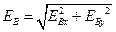 
.
С учетом всех полученных выражений, проделав алгебраические преобразования, получим окончательное выражение для вычисления искомой величины:
.
Вычислим численное значение напряженности суммарного поля в точке В:
Окончательно получаем 
.
Примечание. В некоторых случаях, когда решение связано с достаточно громоздкими алгебраическими преобразованиями, можно проводить расчеты по ходу решения задачи. Так можно было поступить и при решении этой задачи.
Ответ: напряженность электрического поля в точке А равна
Е А = 50.4 кВ/м и направлена от заряда q 1 к заряду q 2. В точке В напряженность равна Е В = 24,1 кВ/м и ее направление показано на рисунке.
Пример 3. 1 Две длинные одноимённо заряженные нити расположены на расстоянии r 1= 10см друг от друга. Линейные плотности зарядов одинаковы и равны 
= 
=10мкКл/м.
Найти модуль и направление напряжённости результирующего поля в точке А, удалённой от каждой нити на расстояние а = 10см.
Анализ:
| Дано: | |||
| r | =10см =20см =10мкКл/м | ||
| r2 | |||
 =
| |||
| a | =10см | ||
| 1) E -? 2) A -? | |||
Электростатические поля, создаваемые различными распределениями зарядов, по принципу суперпозиции складываются в каждой точке пространства. Учитывая симметрию задачи, сделаем рисунок, расположив нити перпендикулярно плоскости чертежа. Точка А удалена от обеих нитей на расстояние а=r 1.Получили равносторонний треугольник. Для того, чтобы найти направление вектора напряжённости поля, создаваемого в точке А зарядом каждой нити, поместим в эту точку пробный заряд «+1» и определим, как поля нитей действуют на этот заряд. Так как нити заряжены положительно, то они будут отталкивать пробный заряд и вектора 
и 
будут направлены так, как показано на рисунке. Вектор напряжённости суммарного поля, согласно принципу суперпозиции, находится по правилу параллелограмма.
Сила взаимодействия этих заряженных нитей зависит от расстояния между ними, поэтому работу сил электростатического поля при раздвижении нитей надо вычислять через интеграл.
Решение:
1) Из рисунка видно, что 
направлен вправо, и модуль его можно найти как:
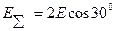
т.к.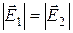 
и 
, где k= 
.
Окончательно получаем
.
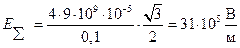2) Сила взаимодействия заряженных нитей зависит от расстояния между ними. Каждая нить создаёт поле, и это поле действует на заряд другой нити. 
- напряженность поля первой нити.
-сила, действующая на единицу длины второй нити равна:
Работу этой силы можно вычислить как:
.
Возьмём интеграл от этой функции. Все постоянные величины выносим за знак интеграла и получаем табличный интеграл, который равняется натуральному логарифму аргумента.
Подставим пределы интегрирования и окончательно получаем:
.
Используя данные задачи, получим численный ответ
Ответ: 1) 
2) 
Поиск по сайту: