 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Энергия заряженного проводника и конденсатора
Заряд, находящийся на проводнике можно рассматривать, как систему взаимодействующих между собой точечных зарядов. Такая система обладает потенциальной энергией. Потенциальной энергией, которой обладает заряженный проводник в отсутствии внешнего электрического поля, называется собственной энергией проводника. Энергия уединенного заряженного проводника может быть определена по одной из формул
,
где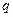 
- заряд проводника, 
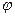- потенциал проводника, 
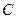- электроемкость проводника.
Энергия конденсатора, т.е. системы, состоящей из двух проводников, может быть определена по следующим формулам
,
где 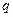- величина заряда одной обкладки конденсатора, 
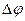- разность потенциалов между обкладками конденсатора, 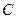- электроемкость конденсатора.
В случае плоского конденсатора энергия модет быть вычислена следующим образом
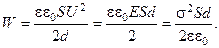
Поиск по сайту: